Divisibility Rules of Numbers from 1 to 19
- Divisibility rule for 1
- Divisibility rule for 2
- Divisibility rule for 3
- Divisibility rule for 4
- Divisibility rule for 5
- Divisibility rule for 6
- Divisibility rule for 7
- Divisibility rule of 8
- Divisibility rule for 9
- Divisibility rule for 10
- Divisibility rule for 11
- Divisibility rule for 12
- Divisibility rule for 13
- Divisibility rule for 14
- Divisibility rule of 15
- Divisibility rule of 16
- Divisibility rule for 17
- Divisibility rule for 18
- Divisibility rule of 19
In this topic – ‘Divisibility Rules of 1, 2, 3…….19’ we are going to learn about the rules of divisibility of natural numbers from 1 to 19. By understanding these rules, we can quickly find out if a given number is divisible by a number or not.
Every student must learn these rules because it helps to avoid lengthy calculations or long divisions. These rules are helpful for quick conclusions which can save time in competitive exams. Let’s learn and understand divisibility rules in-depth with the help of solved examples.
Divisibility rule of 1
All the numbers are divisible by 1. Any number divided by 1 will give itself as a quotient.
Example: Which of the following numbers are divisible by 1
7382575892, 3748, 86940, 0
Solution: All the numbers given above are divisible by 1.
Divisibility rule of 2
All even numbers are divisible by 2 or we can say that if the last digit of any number is an even number, i.e., 0, 2, 4, 6 or 8, then the number is divisible by 2.
To check for the divisibility by 2, just pick the last digit of a number and see if it is divisible by 2 or not. If it is divisible by 2, then the number will also be divisible by 2.
Example: Find out which of the given number(s) is/are divisible by 2:
- 7396
- 573582
- 67729
- 653978
Solution:
7396 is divisible by 2 as the last digit of the given number is 6 (even).
573582 is divisible by 2 as the last digit of the given number is 2 (even).
67729 is not divisible by 2 as the last digit of the given number is 9 (odd).
653978 is divisible by 2 as the last digit is 8 (even).
Example: If 4356x8 and 9823y are divisible by 2. What will be the possible value of x and y:
Solution:
Let us check for 4356x8
x is at ten’s place in the number. Therefore, any value from 0 to 9 is possible for x. As per the divisibility rule for 2, the unit place digit of the number needs to be even to be divisible by 2.
Let us check for 9823y
y is present in the unit place. So, x can be 0 or any even number. So, y can be either 0, 2, 4, 6, or 8.
Divisibility rule of 3
If the sum of all the digits of a number is divisible by 3 then the given number will be divisible by 3.
Let us understand the procedure to check the divisibility by 3 through some examples:
Example: Which of the following numbers are divisible by 3:
1896, 255648, 189773
Solution:
1896:
Sum of all the digits of the number = 1 + 8 + 9 + 6 = 24
As we know, 24 is divisible by 3. Therefore, 1896 is divisible by 3.
255648:
Sum of all the digits of the number = 2 + 5 + 5 + 6 + 4 + 8 = 30
As we know, 30 is divisible by 3. Therefore, 255648 is divisible by 3.
189773:
Sum of all the digits of the number = 1 + 8 + 9 + 7 + 7 + 3 = 35
As we know, 35 is not divisible by 3. Therefore, 255648 is not divisible by 3.
Example: What will be the value of x so that the given numbers are divisible by 3?
- 736x
- 6798y3
Solution:
Let us find the value of x:
As per the divisibility rule for 3, we need to check the sum of digits of the number.
For 736x: Sum of digits = 7 + 3 + 6 + x = 16 + x
If the sum of 16 + x is divisible by 3 only then the number will be divisible by 3. So, the value of x can be 2, 5, or 8 so that the sum of digits is 18, 21, or 24.
For 6798y3: Sum of digits = 6 + 7 + 9 + 8 + y + 3 = 33 + y
If the sum of 33 + y is divisible by 3 only then the number will be divisible by 3. So, the value of y can be 0, 3, 6, or 9 so that the sum of digits is 33, 36, 39, or 42.
In the above example, we can notice that there are multiple values of x and y possible. It needs to be taken care of in questions like this because there can be multiple values the sum of digits that can be divisible by 3.
Divisibility rule of 4
If the last two digits of a given number are divisible by 4 then the number is divisible by 4. The number having two or more zeroes at the end is also divisible by 4.
Let us understand the procedure to check the divisibility by 4 using the below-given examples:
Example: Which of the following numbers is/are not divisible by 4?
- 9258
- 794032
- 1400676
- 43216
Solution:
- 9258 - the last two digits, i.e., ‘58’ is not divisible by 4. Therefore, 9258 is not divisible by 4.
- 794032 - the last two digits, i.e., ‘32’ is divisible by 4. Therefore, 794032 is also divisible by 4.
- 1400676 - the last two digits, i.e., ‘76’ is divisible by 4. Therefore, 1400676 is also divisible by 4.
- 43216 - the last two digits, i.e., ‘16’ is divisible by 4. Therefore, 43216 is also divisible by 4.
Example: If the following numbers are divisible by 4. What needs to be the value of x, y and z in the given number(s):
- 7635x8
- 987263y
- 1275z80
Solution:
- 7635x8
If the last two digits, i.e., x8 are divisible by 4 then the number is divisible by 4
The possible values of x are 0, 2, 4, 6, and 8.
- 987263y
If the last two digits, i.e., 3y are divisible by 4 then the number is divisible by 4
The possible values of y are 2 and 6.
- 1275z80
If the last two digits are divisible by 4 then the number is divisible by 4. In the given number last two digits, i.e., 80 are already divisible by 4.
Therefore, z can have any value from 0 to 9.
Divisibility rule of 5
All the numbers having 0 or 5 as their last digit are divisible by 5.
Example: Which of the following numbers will be divisible by 5:
759265, 5500056, 973180, 564325
Solution:
As we can see that the last digit of 759265, 973180 and 564325 are 5, 0 and 5 respectively. Therefore, these numbers are divisible by 5. The last digit of 5500056 is 6, therefore, it is not divisible by 5.
Example: What is the smallest value possible for x in the number 3x465 to be divisible by 5?
Solution:
Applying the divisibility rule of 5, the number is always divisible by 5 as the last digit of the given number is 5. Hence, the smallest possible value for x is 0.
Divisibility rule of 6
If the given number is divisible by 2 and 3 both. Therefore, the number is divisible by 6.
Note:
Using the Divisibility rule of 2 and divisibility rule of 3, we can say that If a number is even and the sum of its digits is divisible by 3, then the number will be divisible by 6.
Let us understand the procedure to check the divisibility by 6 through the following examples:
Example: Which of the following number(s) is/are divisible by 6?
372, 7380, 86930, 68363
Solution:
The first step is to check if the number is even or odd.
Looking at the last digits of the numbers, 68363 is an odd number, and 372, 7380 and 86930 are even.
Hence, 68363 is not divisible by 6, and 372, 7380 and 86930 will be checked further for divisibility by 3.
The second step is to check if the sum of digits of the number is divisible by 3.
372: 3 + 7 + 2 = 12
Since 12 is divisible by 3, The given number 372 is divisible by 3.
7380: 7 + 3 + 8 + 0 = 18
Since 18 is divisible by 3, The given number 7380 is divisible by 3.
86930: 8 + 6 + 9 + 3 + 0 = 26
Since 26 is not divisible by 3, The given number 86930 is not divisible by 3.
Hence, 372 and 7380 are divisible by 6 out of the given numbers.
Example: If the following numbers are divisible by 6. What should be the smallest possible value of x and y?
- 4562x
- 321y4
Solution:
Applying the divisibility rule of 6 to 4562x
Divisibility by 2:
Any even number (0, 2, 4, 6, 8) is possible for the value of x to make it an even number.
Divisibility by 3:
Let us check the sum of digits: 4 + 5 + 6 + 2 + x = 17 + x
The smallest possible value x among 0, 2, 4, 6 and 8 is 4, for which x + 17 will be 21, i.e., divisible by 3. Therefore, the smallest possible value of x is 4 for the number to be divisible by 6.
Applying the divisibility rule of 6 to 321y4
Divisibility by 2:
As the last digit of the given number is even. So, y can have any value from 0 to 9.
Divisibility by 3:
Let us check the sum of digits: 3 + 2 + 1 + x + 4 = 10 + x
The possible values of y can be 2, 5 and 8, for which 10 + y will be 12, 15 and 18 respectively, i.e., divisible by 3. Therefore, the smallest possible value of y is 2 for the number to be divisible by 6.
Divisibility rule of 7
The divisibility rule for 7 is a lengthy process that is formulated through the concept of oscularity. All steps to check divisibility by 7 are simplified below:
- Take the last digit of the given number and multiply it by 2.
- Now subtract the result of multiplication from the remaining number (excluding the last digit).
- If the resulting number after subtraction can be checked easily if it is divisible by 7, then go to step 4, otherwise go to step 1 with the resulting number after subtraction.
- If the result after subtraction is divisible by 7, then the original number is divisible by 7. If the result after subtraction is not divisible by 7 then the original given number is not divisible by 7.
Repeat the above steps till you are not sure that the result of the 2nd step is divisible or not divisible by 7.
Note: To know why we multiply the last digit with 2 read about the concept of Oscularity. Here, the osculator of 7 is 2.
Let us understand the procedure to check divisibility by 7 through the following examples:
Example: Which of the given number(s) are divisible by 7?
14763, 234635
Solution:
Applying the divisibility rule for 7 in the given numbers:
14763:
Take the last digit of the given number, i.e., 3
multiplying it by 2 and subtracting through remaining number, we get
1476 - 6 = 1470
1470
Repeating the above two steps till we find a recognizable number that is or is not divisible by 7
147 – 0*2 = 147
14 – 7*2 =0
Since 0 is divisible by 7
Therefore, 14763 is also divisible by 7.
234635:
Take the last digit of the given number, i.e., 5
multiplying it by 2 and subtracting through remaining number, we get
23463 - 5*2 = 23453
Repeating the above two steps till we find a recognizable number that is or is not divisible by 7
2345 – 3*2 =2339
233 – 9*2 = 215
21 – 5*2 = 11
Since, the result of the last step, i.e., 11 is not divisible by 7.
Therefore, 234635 is not divisible by 7.
Divisibility rule by 8
A number is divisible by 8 if the last three digits of a number are divisible by 8.
If there is any number with three zeroes as its last three digits, then it must be divisible by 8 as ‘000’ is divisible by 8. Therefore, numbers like 1000, 2000, 10000, 846828478000, …… are divisible by 8.
Let us understand the procedure to check the divisibility by 8 through some examples:
Example: Among 765232, 983412 and 3266, which numbers are divisible by 8?
Solution:
As per the divisibility rule of 8, let us check the last three digits of the given numbers.
765232: Last three digits - 232 is divisible by 8. Therefore, 765232 is divisible by 8.
983412: Last three digits – 412 is divisible by 8. Therefore, 983412 is divisible by 8.
3266: Last three digits – 266 is not divisible by 8. Therefore, 3266 is not divisible by 8.
Example: What is the possible values of x in the following numbers to be divisible by 8:
- 31531x
- 892x46
Solution:
- 31531x
By applying the divisibility rule for 8, the last three digits of 31531x must be divisible by 8.
So, 31x needs to be divisible by 8.
Here, x can be 2.
- 892x46
Last three digits - x46 need to be divisible by 8. No value of x can make it possible for the x46 to be divisible by 8.
Here, it can be noted that the last two digits 46 are not divisible by 4, therefore, the number cannot be divisible by 4 and if a number is not divisible by 4, it cannot be divisible by 8, 16, 32, 64, etc.
Divisibility rule of 9
If the sum of all the digits of a number is divisible by 9. Then, the number is also divisible by 9.
Let us understand the procedure to check the divisibility by 9 through the following examples:
Example: Which of the following number(s) are divisible by 9:
763875, 92376, 987853
Solution:
Let us check the divisibility by 9 by using the divisibility rule for 9:
We need to check the sum of digits and whether the sum of digits is divisible by 9 or not.
763875: 7+6+3+8+7+5 = 36
The Sum of all digits is divisible by 9. Therefore, 763875 is divisible by 9.
92376: 9+2+3+7+6=27
The Sum of all digits is divisible by 9. Therefore, 92376 is also divisible by 9.
987853: 9+8+7+8+5+3 = 40
The Sum of all digits is not divisible by 9. Therefore, 987853 is also not divisible by 9.
Example: What will be the smallest value of x in the number 876x5 to be divisible by 9?
Solution:
Using the divisibility rule of 9, the sum of digits of 876x5 should be divisible by 9.
Sum of all the digits of the given number = 8+7+6+x+5
= 26+x
The smallest possible value of x for the sum of all the digits of the given number is divisible by 9 is 1. At x = 1, the sum of digits will be 27, which is divisible by 9.
Divisibility rule of 10
If a number has the last digit as zero. Then the given number is always divisible by 10.
Example: Which of the following numbers are divisible by 10:
763470, 98234380, 2343335
Solution:
Out of the given numbers, 234335 does not have 0 as the last digit and the other two numbers have the last digit as 0. Therefore, 763470 and 98234380 are divisible by 10.
Divisibility rule of 11
If the difference between the sum of digits at odd places in the number and the sum of digits at even places in the number is divisible by 11. Then, the given number is divisible by 11.
Let us understand the application of the divisibility rule for 11 through the following examples:
Example: Which of the following number(s) is/are divisible by 11:
958793, 71339488, 292839
Solution:
- 958793
Sum of digits at odd places = 9 + 8 + 9 = 26
Sum of digits at even places = 5 + 7 + 3 = 15
Difference between the Sum of digits at the odd place and the Sum of digits at the even place = 26 – 15 = 11
Since, the difference is divisible by 11. Therefore, the number is also divisible by 11.
- 71339488
Sum of digits at odd places = 7 + 3 + 9 + 8 = 27
Sum of digits at even places = 1 + 3 + 4 + 8 = 18
Difference of Sum of the digits at the odd place and the Sum of digits at the even place = 27 - 18 = 9
Since, the difference is not divisible by 11. Therefore, the number is also not divisible by 11.
Example: What will be the value of x in the given number x4969 for the number to be completely divisible by 11?
Solution:
Sum of digits at odd places = x + 9 + 9 = 18 + x
Sum of digits at even places = 4 + 6 = 10
Difference of sum of digits at the odd place and the sum of digits at even place = 18 + x - 10 = 8+x
At x = 3, difference would be 11. The smallest possible value of x is 3 for the number to be divisible by 11.
Divisibility rule of 12
If the given number is divisible by both 3 and 4. Then, the given number is divisible by 12.
Note:
To check the divisibility by 12, firstly check if the number is even, then check if the last two digits are divisible by 4, and at last check if the sum of digits is divisible by 3.
If the given number is ending with an odd digit. Then, the number will never be divisible by 12.
Let us understand the procedure to check the divisibility by 12 through the following Example:
Example: Which of the following numbers are divisible by 12:
643784, 9763124, 789342, 136863
Solution:
Firstly, we can check if the number is even or odd. 136863 is odd and hence not divisible by 12.
Now we are left with three numbers - 643784, 9763124 and 789342
Using the divisibility rule for 4, let us check the last two digits of these numbers:
643784 – Last two digits, 84 are divisible by 4
9763124 - Last two digits, 24 are divisible by 4
789342 - Last two digits, 42 are not divisible by 4
Now, we are left with 643784 and 9763124. Let us proceed with applying the divisibility rule for 3:
643784: Sum of digits is 6 + 4 + 3 + 7 + 8 + 4 = 32
9763124: Sum of digits is 9 +7 + 6 + 3 + 1 + 2 + 4 = 32
Since the sum of all digits of 643784 and 9763124 is divisible by 3. Therefore, the numbers are divisible by 3.
Since 643784 and 9763124 are divisible by 3 and 4 both, we can say that 643784 and 9763124 are divisible by 12.
Example: What will be the value of x in the given number 11713x to be completely divisible by 12?
Solution:
Applying the divisibility rule by 12, we can say that 11713x is divisible by 3 and 4 both.
x can only be 0, 2, 4, 6, or 8.
Using the divisibility rule of 3
Sum of digits: 1 + 1 + 7 + 1 + 3 + x = 13 + x
13 + x is divisible by 3. Here, x can be 2 to make 13 + x divisible by 3.
Using the divisibility rule of 4
Last two digits, 3x is divisible by 4.
At x = 2, 32 is divisible by 4. Hence, the smallest possible value of x is 2 for the number to be divisible by 12.
Divisibility rule of 13
Follow the following step to find out the divisibility by 13:
- Take the last digit of the given number and multiply it by 4.
- Now add the result of multiplication to the remaining number (excluding the last digit).
- If the resulting number after addition can be checked easily if it is divisible by 13, then go to step 4, otherwise go to step 1 with the resulting number after addition.
- If the result after addition is divisible by 13, then the original number is divisible by 13. If the result after addition is not divisible by 13 then the original given number is not divisible by 13.
Repeat the above steps till you don’t find a recognizable number that you can check for divisibility by 13 in the 3rd step.
Note: To know why we multiply the last digit with 4 read about the concept of Osculator. Here, the osculator value of 13 is 4.
Let us understand the procedure to check the divisibility by 13 through the following examples:
Example: Which of the following numbers are divisible by 13:
19747 and 61528
Solution:
Applying the divisibility rule for 13 in each number one by one:
19747:
Step 1: Take the last digit of the number, i.e., 7, and multiply it by 4 will give 28
Step 2: Adding the result of multiplication to the remaining number.
1974 + 7 * 4 = 1974 + 28 = 2002
Repeating the above steps,
2002: 200 + 2 * 4 = 20 + 8 = 208
Again repeat the Step 1 and Step 2,
208: 20 + 8 * 4 = 20 + 32 = 52
Since the result of the above addition is divisible by 13.
Therefore, 19747 is also divisible by 13.
61528:
Step 1: Take the last digit of the number, i.e., 8 and multiply it with 4 will give 32
Step 2: Adding the result of multiplication to the remaining number.
6152 + 8 * 4 = 6152 + 32 = 6184
Repeating the above steps,
6184: 618 + 4 * 4 = 618 + 16 = 634
Again repeat the Step 1 and Step 2,
634: 63 + 4 * 4 = 63 + 16 = 79
Since the result of the above addition is not divisible by 13.
Therefore, 61528 is also not divisible by 13.
Example: What will be the missing value of x in the given number x2082 to be divisible by 13?
Solution:
Let us apply the divisibility rule by 13 to x2082
Take the last digit of the number, i.e., 2, and multiply it with 4
Now, x208 + 8 = x216 (Adding the result of multiplication to the remaining number)
Repeating the above steps
x216: Last digit of above-obtained number 6 * 4= 24
x21+24 = x45 (Adding the result of multiplication from the above step)
x45: Last digit of the above-obtained number 5 * 4= 20
x4+ 20 = x4+20
Here try every value for x from 0 to 9 to find the smallest value of x for which x4 + 20 is divisible by 13.
At x = 0, 1, 2, 3…..9,
x4 + 20 will be 24, 34, 44, 54, …….114
At x = 8, the sum 104 will be divisible by 13.
Hence, the smallest value of x is 8, to make x2082 divisible by 13.
Divisibility rule of 14
If the number is divisible by both 2 and 7 then the given number is divisible by 14.
Note: Since divisibility by 2 is a must condition for a number to be divisible by 14, only an even number is divisible by 14. So, if the last digit of a number is odd then the number will never be divisible by 14.
Example: Which of the following number is divisible by 14:
71876, 405722, 118983
Solution:
Applying the divisibility rule for 14:
Using the divisibility rule for 2, we can see that 118983 is an odd number so, it is not divisible by 14. Now we will check 71876 and 505722 for divisibility by 7.
71876:
Take the last digit of the given number, i.e., 6
multiplying it by 2, and subtracting through remaining number, we get
7187 - 12 = 7175
7175
Repeating the above two steps till we find a recognizable number that is or is not divisible by 7
717 – 5*2 = 707
70 – 7*2 = 56
Since 56 is divisible by 7
Therefore, 71876 is also divisible by 7.
Hence, 71876 is also divisible by 14.
405722:
Take the last digit of the given number, i.e., 2
multiplying it by 2 and subtracting through remaining number, we get
40572 - 2*2 = 40568
Repeating the above two steps till we find a recognizable number that is or is not divisible by 7
4056 – 8*2 = 4040
404 – 0*2 = 404
40 – 4*2 = 32
Since, the result of the last step, i.e., 32 is not divisible by 7.
Therefore, 405722 is not divisible by 7 and not divisible by 14 also.
Example: What will be the value of x in the given number 7191x to be completely divisible by 14?
Solution:
x1912
Using the divisibility rule of 2
As the last digit is even, x1912 satisfies the divisibility rule of 2.
Using the divisibility rule of 7
Take the last digit of the given number, i.e., 2
multiplying it by 2, and subtracting through remaining number, we get
x191 - 4 = x187
x187
Repeating the above two steps till we find a recognizable number that is or is not divisible by 7
x18 – 7*2 = x04
x0 – 4*2 = ?
Let us check for values of x = 0, 1, 2, ……9
We get x0 – 8 as -8, 2, 12, 22, 32, 42, 52, 62……. 82
At x = 5, x1912 is divisible by 7 and hence divisible by 14.
Divisibility rule for 15
If the given number is divisible by both 3 and 5 then the number is divisible by 15.
Note: As we know that divisibility rule of 5 says that the last digit of the number should be 0 or 5, so if the last digit of the given number is 0 or 5 only then find out the sum of all digits of the given number to check the divisibility by 3.
Example: Which of the following number is divisible by 15:
67452147, 117540, 95175
Solution:
Applying the divisibility rule for 15, we can say that 67452147 is not divisible by 15 as the last digit is neither 0 nor 5. Now, we will check for the divisibility by 3 for 117540 and 95175
Using the divisibility rule of 3
117530: 1 + 1 + 7 + 5 + 3 + 0 = 17
95175: 9 + 5 + 1 + 7 + 5 = 27
As we can see that the sum of digits of 117530 is not divisible by 3 and the sum of digits of 95175 is divisible by 3, therefore, 95175 is divisible by 15.
Example: If the given number 1081x5 is completely divisible by 15. What will be the smallest possible value of x??
Solution:
Checking the divisibility by 5
As number is ending with 5. Therefore, number is divisible by 5 always irrespective of value of x.
Using the divisibility rule of 15
Checking the divisibility by 3
1 + 0 + 8 + 1 + x + 5 = 15 + x
Here, possible values of x for the number to be divisible by 3 are 0, 3, 6, and 9.
Hence the smallest value of x is 0 for which 1081x5 is divisible by 15.
Divisibility rule for 16
If the last 4 digits of the given number are divisible by 16. Then the given number is divisible by 16.
Note: If a number is divisible by 16, then it must be divisible by 2, 4, and 8 as well. You can use this to check for divisibility by 16 in some cases to quickly tell about divisibility. Remember that a number can be divisible by 2, 4, and 8 but still not divisible by 16. So, it is a condition that can be used to tell that a number is not divisible by 16 but cannot tell if a number is divisible by 16.
Example: Which of the following number is divisible by 16:
21824, 72304, 413376
Solution:
21824
Take the last 4 digits of the given number, i.e., 1824
Dividing 1824 by 16, we get 114
Since the last 4 digits of 21824 are divisible by 16, 21824 will also be divisible by 16.
72304
Take the last 4 digits of the given number, i.e., 2304
Dividing 2304 by 16, we get 144
Since the last 4 digits of 72304 are divisible by 16, 72304 will also be divisible by 16.
413366
Here we can observe that the last two digits, i.e., 66 are not divisible by 4, so, we can say that the number 413366 is not divisible by 4 and also not by 16.
Example: If the given number 15769x is divisible by 16. What is the missing value of x?
Solution:
As we know that to be divisible by 16, a number should be divisible by 2, 4 and 8 also.
Divisibility by 4:
If we take the last two digits, i.e., 9x, to be divisible by 4, x should be 2, 6, or 8.
Divisibility by 8:
If we take the last two digits, i.e., 69x, to be divisible by 8, x should be 6.
Here we can say that x should be 6 without checking further.
We can follow the method to check the divisibility by 16 directly:
Taking the last four digits of the number and dividing it by 16
Since 1x is the remainder in the division of the last 4 digits.
So, for 15769x to be divisible by 16, x should be 6.
Divisibility rule of 17
To find out the divisibility by 17 follow the following step:
- Take the last digit of the number and multiply it by 5.
- Now, subtract the result of multiplication from the remaining number. (Excluding the last digit)
- If the resulting number after subtraction can be checked easily if it is divisible by 17, then go to step 4, otherwise go to step 1 with the resulting number after subtraction.
- If the result of subtraction is divisible by 17 then the given number is divisible by 17 and if not, then the number is not divisible by 17.
Repeat the above steps till you don’t find a recognizable number that you can check for divisibility by 17 in the 3rd step.
Note: To know why we multiply the last digit with 5 read about the concept of Osculator. Here, the osculator value of 17 is 5.
Example: Which among the following will be divisible by 17:
145197, 7128, 108647
Solution:
145197:
Taking the last digit of the number, i.e., 7, and multiplying it with 5
14519 - 7*5= 14484
Repeating the above two steps:
1448 – 4 * 5 = 1428
142 – 8 * 5 = 102
10 – 2 * 5 = 0
Since 0 is divisible by 17. Therefore, 145197 is divisible by 17.
7128:
Taking the last digit of the number, i.e., 8, and multiplying it with 5
712 – 8 * 5 = 672
Repeating the above two steps
67 – 2 * 5 = 57
Since 57 is not divisible by 17. Therefore 7128 is not divisible by 17.
108647:
Taking the last digit of the number, i.e., 7, and multiplying it with 5
10864 – 7 * 5 = 10829
Repeating the above two steps
1082 – 9 * 5 = 1037
103 – 7 * 5 = 68
Since 68 is divisible by 17. Therefore, 108647 is divisible by 17.
Example: What will be the missing value of x for the given number x579 to be completely divisible by 17?
Solution:
Using the divisibility rule of 17
Taking the last digit of the number, i.e., 9, and multiplying it with 5
x57 – 9 * 5 = x12
x1 – 2 * 5
Try numbers from 0 to 9 for the result of subtraction to be divisible by 17
x as 1: 11 - 10 = 1 (Not divisible by 17)
x as 2: 21 - 10 = 11 (Not divisible by 17)
x as 3: 31 - 10 = 21 (Not divisible by 17)
x as 4: 41 - 10 = 31 (Not divisible by 17)
x as 5: 51 - 10 = 41 (Not divisible by 17)
x as 6: 61 - 10 = 51 (divisible by 17)
Hence, the value of x will be 6 to make x579 divisible by 17.
Divisibility rule of 18
If a given number is divisible by 9 and 2, then the number is divisible by 18.
As per the divisibility rule of 2, a number needs to be even to be divisible by 2. So, an even number that is divisible by 9, is also divisible by 18.
Let us understand the divisibility rule for 18 through the following examples:
Example: Which of the following number are divisible by 18:
9504, 1710763, 362834
Solution:
Firstly, we need to check if the number is even or odd. As 9504 and 363844 are even, we will check further for their divisibility by 9 by checking the sum of digits.
9504: 9 + 5 + 0 + 4 = 18 (Sum of all digits is divisible by 9)
362834: 3 + 6 + 2 + 8 + 4 + 3 = 26 (Sum of all digits is not divisible by 9)
Therefore, we can say that out of the given numbers, 9504 is divisible by 18.
Example: What will be the value of x in the given number 9261x so that it is divisible by 18?
Solution:
Using the divisibility rule of 2
Possible value of x for the number to be divisible by 2 is 0, 2, 4, 6 and 8.
Using the divisibility rule of 9
9 + 2 + 6 + 1 + x = 18 + x
The value of x possible here is 0 for the number to be divisible by 9.
Hence, the smallest possible value of x is 0 for the number to be divisible by 18.
Divisibility rule for 19
Follow the following step to find out the divisibility by 19:
- Take the last digit of the given number and multiply it by 2.
- Now add the result of multiplication to the remaining number (excluding the last digit).
- If the resulting number after addition can be checked easily if it is divisible by 19, then go to step 4, otherwise go to step 1 with the resulting number after addition.
- If the result after addition is divisible by 19, then the original number is divisible by 19. If the result after addition is not divisible by 19 then the original given number is not divisible by 19.
Repeat the above steps till you don’t find a recognizable number that you can check for divisibility by 19 in the 3rd step.
Example: Which of the following number are divisible by 19:
49096, 23613
Solution:
Applying the divisibility rule for 19 in each number one by one:
49096:
Step 1: Take the last digit of the number, i.e., 6, and multiply it by 2 will give 12
Step 2: Adding the result of multiplication to the remaining number.
4909 + 6 * 2 = 4909 + 12 = 4921
Repeating the above steps,
4921: 492 + 1 * 2 = 492 + 2 = 494
Again, repeat the Step 1 and Step 2,
494: 49 + 4 * 2 = 49 + 8 = 57
Since the result of the above addition is divisible by 19.
Therefore, 49096 is also divisible by 19.
23613:
Step 1: Take the last digit of the number, i.e., 3 and multiply it with 2 will give 6
Step 2: Adding the result of multiplication to the remaining number.
2361 + 3 * 2 = 2361 + 6 = 2370
Repeating the above steps,
2370: 237 + 0 * 2 = 237 + 0 = 237
Again, repeat the Step 1 and Step 2,
237: 23 + 7 * 2 = 23 + 14 = 37
Since the result of the above addition is not divisible by 19.
Therefore, 23613 is also divisible by 19.
Example: What will be the value of x in the given number x8582 to make it completely divisible by 19?
Solution:
Using the divisibility rule of 19
Taking the last digit of the given number, i.e., 2
multiplying it with 2 and adding it to the remaining number.
Now, x858 + 2 * 2 = x862
Now, repeat the above steps
X86 + 2 * 2 = x90
X9+ 0 = x9
The smallest possible value of x to make the result of addition to be divisible by 19 is 1. Therefore, the smallest possible value for x is 1 for x8582 to be divisible by 19.
|
Divisibility |
Rule |
Example |
|
Divisibility rule of 1 |
All the numbers are divisible by 1. |
56,179 |
|
Divisibility rule of 2 |
The last digit of the number should be even. |
76352, 7382, 9716 |
|
Divisibility rule of 3 |
The sum of all the digits of the number is divisible by 3. |
7293: 7+2+9+3= 21 29151: 2+9+1+5+1= 18 |
|
Divisibility rule of 4 |
The last two digits of the number are divisible by 4. |
9712: 12 is divisible by 4.
|
|
Divisibility rule of 5 |
The last digit of the number should be 0 or 5. |
579865, 79820 |
|
Divisibility rule of 6 |
The last digit is even and the sum of all digits is divisible by 3. |
5838: last digit (8) is even Sum of digits: 5 + 8 + 3 + 8 = 24 is divisible by 3. |
|
Divisibility rule of 7 |
Multiply the last digit by 2 and subtract with the remaining number. The resultant should be divisible by 7. Continue this until you get a sum that can be checked easily to be divisible or not by 7. |
2219: 221-9*2=203 203: 20-3*2= 14 14 is divisible by 7. 2219 is also divisible by 7. |
|
Divisibility rule of 8 |
The last three digits of the number are divisible by 8. |
7896: last three digits 896 are divisible by 8. |
|
Divisibility rule of 9 |
The sum of all digits of the number is divisible by 9. |
5157: 5+1+5+7=18 18 is divisible by 9 and 5157 is divisible by 9. |
|
Divisibility rule of 10 |
The last digit of the number must be 0 only. |
897930, 53630 |
|
Divisibility rule of 11 |
The difference between the sum of odd place digits and even place digits must be divisible by 11. |
98274: (9+2+4) – (8+7) = 0 |
|
Divisibility rule of 12 |
The sum of all digits is divisible by 3 and the last two digits of the number are divisible by 4 |
9096: 9 + 0 + 9 + 6 = 24 96 is divisible by 4. 9096 is divisible by 12. |
|
Divisibility rule of 13 |
Multiply the last digit with 4 and add to the remaining digits. The resultant should be divisible by 13. Continue this until you get a sum that can be checked easily to be divisible or not by 13. |
50661: 5066+4*1=5070 5070: 507 + 4 * 0 = 507 507: 50 + 4 * 7 = 78 78 is divisible by 13. |
|
Divisibility rule of 14 |
The last digit must be even and the number must follow the divisibility rule of 7 |
9128: Last digit 8 is even Checking for divisibility by 7, 9128: 912 – 2 * 8 = 896 896: 89 – 2 * 6 = 77 77 is divisible by 7. So, 9128 will be divisible by 14. |
|
Divisibility rule of 15 |
The sum of all digits of a number must be divisible by 3 and the last digit of the number must be 0 or 5 only. |
46530: 4+6+5+3+0=18. as sum of digits, 18 is divisible by 3 and the last digit is 0. Hence, divisible by 15 |
|
Divisibility rule of 16 |
The last 4 digits of the number must be divisible by 16. |
58832: 8832/16 = 552. Hence, divisible by 16 |
|
Divisibility rule of 17 |
Multiply the last with 5 and subtract it from the remaining number. The resultant should be divisible by 17. Continue this until you get a sum that can be checked easily to be divisible or not by 17. |
11186: 1118 – 5 * 6 = 1088 1088: 108 – 5 * 8 = 68 68 is divisible by 17. 11186 is divisible by 17. |
|
Divisibility rule of 18 |
The last digit is even and the sum of all the digits of the number is divisible by 9. |
7848: 8 is even Sum of digits: 7 + 8 + 4 + 8 = 27 7848 is divisible by 18.
|
|
Divisibility rule of 19 |
Multiply the last digit with 2 and subtract it from the remaining number. If the resultant is divisible by 19, then the number is also divisible by 19. Continue this until you get a sum that can be checked easily to be divisible or not by 19. |
13243: 1324 + 2 * 3 = 1330 1330: 133 + 2 * 0 = 133 133: 13 + 2 * 3 = 19 19 is divisible by 19. So, 13242 will be divisible by 19. |
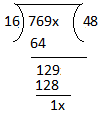




 Latest
Latest 



Comments