Important Concepts and Formulas of Coordinate Geometry

---

A coordinate system is the reference system used to show the coordinates in a meaningful manner. It has a practical application in the field of GPS, printing, computer-aided manufacturing, and a lot more.

Also, Coordinate geometry is a topic asked widely in various government exams. The questions related to coordinate geometry are relatively formula based and on fundamental concepts. In this article, we are going to discuss all the concepts related to Coordinate Geometry and its application on straight lines. So, let’s begin.

Coordinate Geometry is the branch of mathematics related to the study of algebraic equations through the geometrical interpretation. In this branch, we plot the graphs over the three dimensions to show points, lines, curves, planes, surfaces, etc.

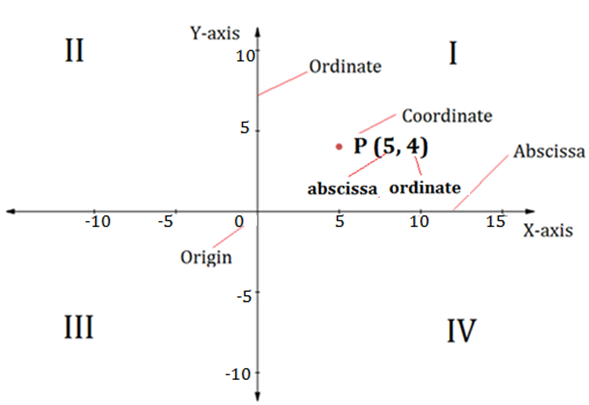
Coordinate: A coordinate contains a group of numbers that contains the information of a point, line, and surfaces on the graph of an equation. A coordinate is represented as (x, y).

The important terms which are related to coordinates are:

Origin: The intersection of all the axes in a graph is known as the origin of that graph. Origin is used as a reference for measuring the distances for coordinates.

Types of Coordinate system

Cartesian coordinate system: A cartesian coordinate system specifies a point by two numbers, which signifies the distance from two perpendicular axes, i.e., X-axis and Y-axis.

Ordinate: In a standard two-dimensional graph, ordinate refers to the vertical axis.

Abscissa: In a standard two-dimensional graph, ordinate refers to the horizontal axis.

The ordinate and abscissa divide the plane into four parts, known as quadrants.

In Quadrant I both X and Y coordinates are positive

In Quadrant II X coordinate is negative while Y coordinate is positive

In Quadrant III X coordinate is positive while Y coordinate is negative

In Quadrant IV both X and Y coordinates are negative

 

Polar coordinate system: Polar coordinates system specifies a point by the distance (r) from a reference point (known as origin or pole) and angle (Ɵ) from an axis.

A point in a polar coordinate system is defined as (r, Ɵ).

 

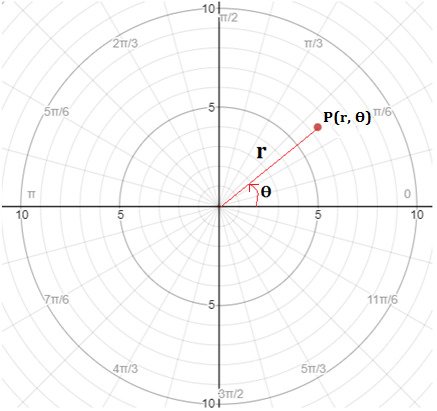
Conversion of Polar coordinates into cartesian coordinates

The conversion of point A (r, Ɵ) in the cartesian coordinate system will be A(x, y)

Where,

x = rcosƟ and y = rsinƟ

\(r=\sqrt{x^{2}+y^{2}} \) and \(tan\theta =\frac{y}{x}\)

Example: Convert the point P(5, 30^o) into cartesian form

Solution

Step 1: Firstly, find the value of x coordinate

We know,

x = rcosƟ

⇒x = 5 cos 30^o

⇒\(x=5* \sqrt{\frac{3}{2}}=2.5* \sqrt{3}\)

Step 2: Secondly, find the value of y coordinate

y = rsinƟ

⇒y = 5 sin 30^o

⇒\(y=5* \frac{3}{2}=2.5\)

Therefore,

\(P(5, 30^{\circ}) \)⇒\(P(2.5 \sqrt{3} ,2.5)\)

Distance between two points:

The distance between two points whose coordinates are A (x₁, y₁)and B (x₂, y₂) will be

\(Distance = \space \sqrt{{(x_{2}-x_{1})}^{2}+{(y_{2}-y_{1})}^{2}}\)

Note: The distance of any point P(x, y) from the origin can be given as

\(Distance= \space \sqrt {(x)^{2}+(y)^{2}}\)

Note: In a polar coordinate system distance between two points A(r₁, Ɵ₁) and B(r₂, Ɵ₂) is given as 

Distance= r₁² + r₂² – 2r₁ r₂ cos (Ɵ₁ – Ɵ₂)

Section Formula: Section formula tells us about the coordinates of the Point, which divides a line segment into the ratio m : n.

• Internal division: The coordinates of the Point A(x, y) which divides the line segment PQ internally in the ratio m : n, as shown in the figure, will be given as

\((x,y)=(\frac {mx_2+nx_1}{m+n},\frac {my_2+ny_1}{m+n})\)

 

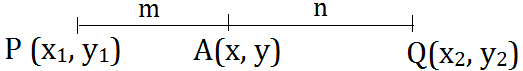
• External division: The coordinates of the Point A(x, y) which divides the line segment PQ externally such that AP : AQ = m : n, as shown in the figure, will be given as

 \((x,y)=(\frac {mx_2-nx_1}{m-n},\frac {my_2-ny_1}{m-n})\)

 

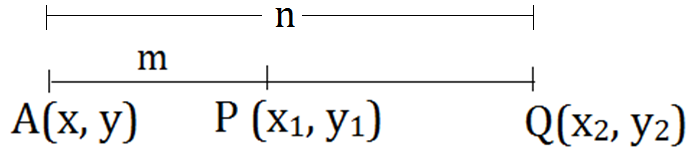
NOTE:

1. The coordinates of a point A(x, y) which divides the line segment PQ into two equal halves (i.e., m : n = 1 : 1) is given as:

\((x,y)=(\frac {x_2+x_1}{2},\frac {y_2+y_1}{2})\)

2. If a point A divides line PQ internally in the ratio m : n and the point B divides the line segment PQ externally in the ratio m : n, then

\(\frac {1}{AP} +\frac {1}{BP}=\frac {2}{PQ}\)

Slope of a Straight Line (m)

The slope of a line denotes the steepness of a line. Slope is the tangent of the angle made by straight line with the positive direction of X-axis.

Slope can also be defined as the change in Y-coordinate per unit change in X-coordinate.

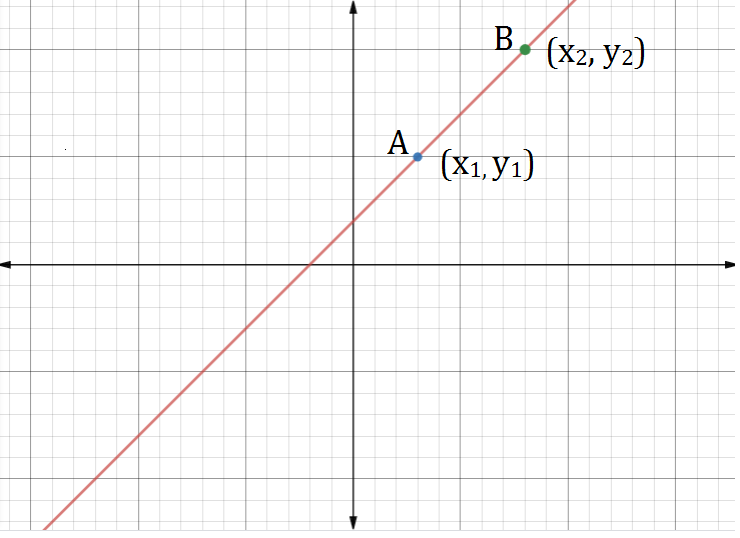
The slope of a line AB having coordinates A(x₁, y₁) and B(x₂, y₂) is given as

\(m=tan\theta =\frac {y_2-y_1}{x_2-x_1}\)

Note: Slope of X-axis is 0 and the slope of Y-axis is not defined.

Example:

Find the slope of the line passing through the coordinates A(1, 9) and B(3, -5)?

Solution

We know,

\(Slope \space (m)=tan\theta =\frac {y_2-y_1}{x_2-x_1}\)

\(So, Slope \space=\space \frac {-5-9}{3-1}=-\frac {14}{2}=-7\)

Thus, slope of the given line will be -7.

Equation of a Straight Line

The equation of line parallel to X-axis is given as y = d

The equation of line parallel to Y-axis is given as x = c

There are many forms a straight line can be represented:

1. Slope form: The equation of straight-line having slope m is given as y = mx + c, where c is the intercept of a straight line on Y-axis.
2. Intercept form: The intercept form of a straight line having a and b as the intercepts on X-axis and Y-axis respectively is given as

\(\frac{x}{a}+\frac{y}{b} = 1\)

3. Point slope form: The equation of line passing through Point (x₁, y₁) and having slope m is given as

\(y-y1=m (x-x1)\)

4. Two-point form: The equation of line passing through points (x₁, y₁) and (x₂, y₂) is given as

\(y-y_1= \frac {y_2-y_1}{(x_2-x_1)}(x-x_1 )\)

5. The General form of a straight line is given as ax + by + c = 0
6. Normal Form: Normal form of any straight line is defined by the length of the perpendicular (p) from the origin to the line and angle (∅) which perpendicular makes with the positive direction of X-axis. Any straight line can be represented in normal form as

x cos ∅ + y sin ∅ = p

Note: The slope of a line can also be defined as the coefficient of x when the coefficient of y is 1.

Example: Find the slope of the equation 3y = 4x + 9

Solution

Step 1: Firstly, make the coefficient of y as 1

3y = 4x + 9

⇒\(y=\frac{4x}{3} \space + \space \frac{9}{3}\)

Step 2: Now, the slope of equation is the coefficient of x i.e. slope (m) = 4/3

Position of pointA(x1, y1) and B(x2, y2) with respect to line ax + by + c = 0

If the value of ax₁ + by₁ + c and ax₂ + by₂ + c are of the same sign than the points lie on the same side of straight-line otherwise on the different side of the line.

Note: For a point (x₁, y₁), if ax₁ + by₁ + c is equal to zero, then the point lies on the line ax + by + c = 0

Angles between two lines

The acute angle between two lines having slopes m₁ and m₂ is given as

\(tan⁡\Theta =\left | \frac{m_2-m_1}{1+m_1 m_2} \right |\)

And, the obtuse angle can be found out directly by subtracting acute angle from 180^o

The acute angle between two lines having equation ax₁ + by₁ + c and equation ax₂ + by₂ + d = 0 will be

\(tan⁡\theta =\left | \frac{b_1 a_2-a_1 b_2}{a_1 a_2+b_1 b_2 } \right |\)

Equation of a line parallel to a line

The family of equation of lines perpendicular to line ax + by + c = 0 is given as ax + by + d = 0

1. When two lines are parallel to each other then, the angle between them is zero and slopes of them are equal, i.e., m₁ = m₂

Equation of a Line perpendicular to a line

The family of equation of lines perpendicular to line ax + by + c = 0 is given as bx – ay + d = 0

1. When two lines are perpendicular, then the angle between them is 90⁰
2. When two lines a₁ x + b₁ y + c = 0 and a₂ x + b₂ y + d are perpendicular, then a₁a₂ + b₁b₂ = 0
3. The product of the slopes of two perpendicular lines is always 1, i.e., m₁­m₂ = -1

Example: If the line formed by the points (1, 4) and (3, k) is perpendicular to the line 3x – 4y = 5, then what will be the value of k?

Solution

Step 1: Find the slope of line 3x – 4y = 5

Slope is the coefficient of x when coefficient of y is 1.

⇒\(y = \frac{3}{4}x-\frac{5}{4}\)

So, slope for line will be m₁ = 3/4

Step 2: Find the slope for line formed by points (1, 4) and (3, k)

⇒\(m_2=\frac{k-4}{3-1}=\frac{k-4}{2}\)

Step 3: for two lines perpendicular to each other m₁ * m₂ = -1

⇒\(\frac{3}{4}*\frac{k-4}{2}=\space -1\)

\(\Rightarrow\begin{alignedat}{2} 3&k- 12 = -8 \\ \end{alignedat}\)

⇒\(k =\frac {4 }{3}\)

Distance of a point from a line

The shortest distance from a point P (x₁, y₁) to the straight line having equation Ax + By + c = 0 will be the length of the perpendicular drawn from point P to the line Ax + By + C = 0

\(Distance=\frac {\left | Ax_1+By_1+C \right | } { \sqrt{A^2+B^2 }}\)

Shortest distance between two parallel lines

The shortest distance between two parallel lines having equations y = mx + c₁ and y = mx + c₂ is given as

\(Distance=\frac {\left | c_1-c_2 \right | }{\sqrt{1+m^2}}\)

The shortest distance between two parallellines having equation Ax + By + C₁ = 0 and Ax + By + C₂ = 0 is given as

\(Distance=\frac {\left | C_1-C_2 \right | }{\sqrt{A^2 + B^2 }}\)

Condition for collinear points

The points are said to be collinear when all the points lie in a straight line.

The points A (x₁, y₁), B (x₂, y₂) and C(x₃, y₃) will be collinear to each other if slope of line segment AB is equal to the slope of line segment BC. Equating slope of both the lines we get a direct result

⇒\(\frac {y_2-y_1}{x_2-x_1}=\frac {y_3-y_2}{x_3-x_2}\)

Condition for concurrent lines

The pair of lines is said to be concurrent to each other if all the lines intersect each other at the common point P, which is known as Point of concurrency.

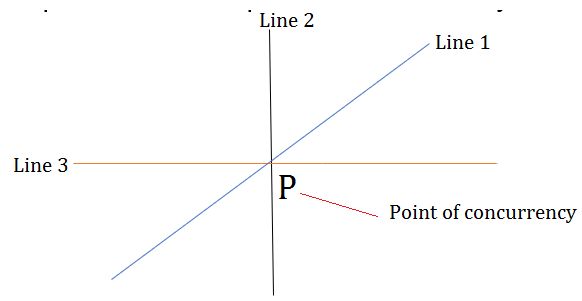
The lines a₁x + b₁y +c₁ = 0, a₂x + b₂y +c₂ = 0 , and a₃x + b₃y +c₃ = 0  will be concurrent to each other if and only if

⇒\(\begin{vmatrix} a_1 &b_1 &c_1 \\ a_2 &b_2 &c_2\\ a_3 &b_3 &c_3 \end{vmatrix} =0\)

Projection of a point on any straight line

To find the projection of a point P (x₁, y₁) on a line Ax + By + C = 0 can be found using the following steps:

Step 1: First find the equation of line perpendicular to Ax + By + C = 0

The line perpendicular to Ax + By + C = 0 will be Bx – Ay + D = 0

Step 2: Now, put the coordinates of point P (x₁, y₁) in the line Bx – Ay + D = 0 as the points satisfy the equation to find the value of D.

⇒ Bx₁ – Ay₁ + D = 0

Step 3: Now, find the intersection point of line Ax + By + C = 0 and Bx – Ay + D = 0 to obtain the projection of a point on a line Ax + By + C = 0

Example: What will be the projection of (3, 1) on the line 5x – 3y = 4?

Solution

Step 1: Equation of Line perpendicular to 5x – 3y = 4 will be

⇒ 3x – 5y = D

Step 2: Putting coordinates of (3, 1) in the above equation to find the value of D

⇒ D = 3 * 3 – 5 * 1 = 9 – 5 = 4

Step 3: Find the intersection point of 5x – 3y = 4 and 3x – 5y = 4

Solving above equation for x and y we get

x = 1/2 and y = -1/2

Thus, projection of (3, 1) on the line 5x – 3y = 4 is \((\frac{1}{2},-\frac{1}{2})\)

Reflection of a point

• The reflection of a point (x₁, y₁) about X-axis is (x₁, - y₁)
• The reflection of a point (x₁, y₁) about Y-axis is (-x₁, y₁)
• The reflection of a point (x₁, y₁) about line y = x is (y₁, x₁)
• The reflection of a point (x₁, y₁) about line y = - x is (-y₁, -x₁)
• The reflection of a point (x₁, y₁) about origin (0, 0) is (-x₁, -y₁)

How to find reflection of a point about any straight line

Step 1: First we have to find the projection of the Point on the line (SEE ABOVE)

Step 2: Now, distance between Point and its projection is similar to the distance between the reflection of Point and projection of Point so using either section formula or formula for distance between two points we can get the coordinates of reflection of a point.

Coordinates of Centroid of a triangle

The coordinates of a centroid of a triangle ABC having vertices as A (x₁, y₁), B (x₂, y₂) and C(x₃, y₃) is given as

⇒\((\frac{x_1+x_2+x_3}{3},\frac{y_1+y_2+y_3}{3})\) 

Coordinates of Incentre of a triangle

The coordinates of an Incentre of a triangle ABC having vertices as A (x₁, y₁), B (x₂, y₂) and C (x₃, y₃) and sides a = BC, b = CA and c = AB is given as

⇒\((\frac{ax_1+bx_2+cx_3}{a+b+c},\frac{ay_1+by_2+cx_3}{a+b+c} )\)

NOTE: Centroid divides the line formed by joining Orthocentre and Circumcentre internally in the ratio 2 : 1.

Area of a triangle

The area of a triangle ABC formed from the vertices A (x₁, y₁), B (x₂, y₂) and C (x₃, y₃) will be

\(Area=1/2 \begin{vmatrix} x_1 &y_1 &1 \\ x_2 &y_2 &1 \\ x_3 &y_3 &2 \end{vmatrix}=\frac{1}{2} \left | x_1 (y_2-y_3 )+x_2 (y_3-y_1 )+x_3 (y_1-y_2 ) \right |\)

Note: The vertices should be taken in either a clockwise direction or an anticlockwise direction.

NOTE: If the area of the triangle is zero, then all the vertices A, B, and C are collinear to each other, i.e., all the points lie on a straight line.

NOTE: The Area of triangle for line y = m₁x + c₁, y = m₂x + c₂ and x = 0 is given as

\(Area=\frac{\left | {c_1}^2-{c_2}^2 \right | } {2(m_1-m_2 ) }\)

Area of a Polygon

The area of a polygon having n vertices in the form (x_i, y_i) where i = 1, 2, 3, ……, n can be calculated as

\(Area=\frac{1} {2} \space \left | \space x_{i}y_{i+1}-y_{i}x_{i+1} \space \right |\)

Example: Find the area of the quadrilateral having vertices (1, 4), (2, 6), (5, 4) and (4, 3)

Solution

Step 1: write x coordinates of all the vertices in a column and write y coordinates of all the vertices in another column. Repeat the coordinates of first point in the last row to complete the calculation of area.

xi	yi
1	4
2	6
5	4
4	3
1	4

 

 

 

                                                                                               
Step 2: Now multiply the first row coordinate of x with second-row coordinate of y and then from the obtained result subtract product of first row coordinate of y and second row coordinate of x. Do the step for all the coordinates and then add all the numbers thus obtained

⇒ (1*6 – 2*4) + (2*4 – 5*6) + (5*3 – 4*4) + (4*4 – 1*3)

⇒ -2 – 22 – 1 + 13

⇒ - 12

Thus, area of quadrilateral will be

⇒\({1 \over 2} \space Obtained \space result={1 \over 2}* \space \left | \space - 12 \space \right | =6 \space\)sq. unit

Share Blog