Ratio and Proportion Definitions, Concepts, Formulas, Tricks and Examples

---

RATIO:

Ratio is a mathematical term to compare two similar quantities expressed in the same units using division. A ratio is typically represented by the symbol ‘:’. A ratio can be treated as a fraction.

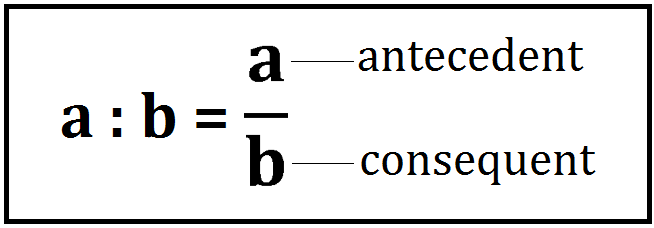
Antecedent: If we write a ratio in terms of fraction, then the numerator in the fraction is known as an antecedent for the ratio. In the given figure, ‘a’ is the antecedent.

Consequent: If we write a ratio in terms of fraction, then the denominator in the fraction is known as consequent for the ratio. In the given figure, ‘b’ is the consequent.

Compound ratio: Ratios are compounded by multiplying together the antecedents for a new antecedent and the consequents for a new consequent.

The compound of (a : b) and (c : d) is \({ac \over bd }\) or (ac : bd).

In case of three ratios (a : b), (c : d), (e : f) compound ratio is (ace: bdf).

Some facts:

1. A ratio can be defined only if two quantities “a” and “b” are in the same units.
2. A ratio is a pure number, i.e., without any unit of measurement.
3. The ratio would stay unaltered even if both the antecedent and the consequent are multiplied or divided by the same number.
4. Inverse ratio is the inverse or transverse nature of a ratio, i.e., inverse ratio of (a : b) is (b : a).

 

Example: - Find the ratio of the ‘9 hour’ and ‘45 seconds’?

a) 1 : 5           b) 9 : 45         c) 12 : 1         d) 720 : 1

Solution: - We know a ratio can be defined only if both the quantities are in the same units

So, 9 hours = 9 * 60 * 60 = 32400 seconds

Thus, ratio of ‘9 hour’ and ‘45 seconds’ will be

⇒ 32400 : 45 = 720 : 1

Thus, correct option is (d).

 

COMPARISON OF RATIOS:

Ratios can be compared to each other on the basis of their numerator and denominator values.

We say that (a: b) > (c: d) ⇒ \({a \over b}>{c \over d}\);

Two or more ratios may be compared by reducing the equivalent fractions to a common denominator and then comparing the magnitudes of their numerator.

# Trick to compare two fractions

To compare two fractions, \({a \over b}\) and \({c \over d}\)

We can compare the fractions \({a \over b-a}\) and\({c \over d-c}\)

If \({a \over b-a}<{c \over d-c}\), then\({a \over b}<{c \over d}\)

 

Example: - Arrange the given numbers in the ascending order \({11 \over 23}, {17 \over 32}, {19 \over 29}\)?

Solution: - Changing all the fractions into the form\({a \over b-a}\) we get 

⇒\({11 \over 23-11}\),\( {17 \over 32-17}\), and\( {19 \over 29-19}\)

We get,

⇒\( {11 \over 13}\),\( {17 \over 15}\), and \( {19 \over 10}\)

⇒\( {11 \over 13}\), \(1.13\), and \(1.9\)

Thus, arranging the given fractions in ascending order, we get

⇒\({11 \over 13}<1.13<1.9\)

Thus, the arrangement of given fractions is

⇒\({11 \over 23}<{17 \over 32}< {19 \over 29}\)

 

CONVERSION OF RATIOS:

Type I: If A : B = x : y and B : C = y : z, then A : B : C can be calculated by modifying the ratios with the equivalent ratios such that the value of B in the ratios become the same.

Example: - If A : B = 4 : 3 and B : C = 6 : 5, then what is the value of A : B : C?

Solution: - To equate the ratios, we should first calculate the LCM of the value of B in both the ratios, i.e., LCM of (3, 6) = 6

Now, multiplying first ratio (A : B) by \({6 \over 3}=2\) and second ratio (B : C) by \({6 \over 6 }=1\)

Therefore,

2 (A : B) = (8 : 6) and B : C = 6 : 5

Therefore, A : B : C = 8 : 6 : 5

 

Type II: If A = 2B = 5C, then in the ratio A : B : C, value corresponding to ‘A’ will be the product of the coefficient of ‘B’ and ‘C’ while value corresponding to ‘B’ will be a product of the coefficient of ‘A’ and ‘C’ and value corresponding to ‘C’ will be a product of the coefficient of ‘A’ and ‘B’

Example: - Find the ratio A : B : C, if 3A = 4B = 2C?

Solution: - Given: 3A = 4B = 2C

Here, coefficient of A is 3, B is 4 and C is 2

So, A : B : C = (4 * 2) : (3 * 2) : (3 * 4)

⇒ A : B : C = 8 : 6 : 12 = 4 : 3 : 6

 

Type III: If A : B : C = (1/a) : (1/b) : (1/c), then to write A : B : C in the integer terms we should multiply all the numerator with the LCM of (a, b, and c)

Example: - Write the ratio A : B : C = (1/3) : (2/7) : (5/6) in the simplified terms

Solution: - Given:  A : B : C = (1/3) : (2/7) : (5/6)

Here, LCM of (3, 7 and 6) = 42

Now, multiplying 42 in the numerator part we get

\(A:B:C=({1 \over 3*42}): ({2 \over 7}*42):({5 \over 6}*42)\)

⇒\(A:B:C=14:12:35\)

 

Properties of Ratio

1. If \(({a \over b}={c \over d})\), then \(({b \over a}={d \over c})\) i.e., the inverse ratios of two equal ratios are equal. The property is called “Invertendo property”.
2. If \(({a \over b}={c \over d})\), then \(({a \over c}={b \over d})\) i.e., the ratio of antecedents and consequents of two equal ratios are equal. This property is called “Alternendo property”.
3. If \(({a \over b}={c \over d})\), then \(({(a+b) \over (b)})=({(c+d) \over (d)})\) This property is called “Componendo theorem”.
4. If \(({a \over b}={c \over d})\), then \(({(a-b) \over (b)})=({(c-d) \over (d)})\) This property is called “Dividendo theorem”.
5. If \(({a \over b}={c \over d})\), then \(({(a+b) \over (a-b)})=({(c+d) \over (c-d)})\) This property is called “Componendo-Dividendo theorem”.

 

Summation of ratios

If there are multiple ratios which are equal to each other, then the ratio of summation of all the numerators in each ratio to summation of all denominators in each ratio will also be equal to the ratios.

Let there are some ratios\({a \over b}={c \over d}={e \over f}....\) equal to each other, then

\(({a \over b}={c \over d}={e \over f}....={a+c+e+... \over b+d+f...})\)

 

Different Operations on Ratios

1. The number \({bc-ad \over c-d}\), when subtracted from numerator and denominator of ratio (a : b), the ratio of the numbers changes to the ratio (c : d).
2. If the ratio between the first and the second numbers is (a : b) and the ratio between the second and third numbers is c : d, then the ratio between all three numbers is given by (ac : bc : bd).
3. If the ratio between the first and the second numbers is (a : b), ratio between the second and third numbers is (c : d) and the ratio between the third and fourth numbers is (e : f), then the ratio between all four numbers is given by (ace : bce : bde : bdf).
4. On adding ‘x’ to the ratio of the two numbers a and b, if the ratio become (c : d) then,

1. Sum of the two numbers will be equal to

\(({x \space (a+b) \space (c-d) \over ad-bc})\)

2. The difference of two numbers will be equal to

\(({x \space (a- b) \space (c-d) \over ad-bc})\)

3. While two numbers are given as

\(a=({{xa \space (c-d) } \over ad -bc})\) & \(b=({{xb \space (c-d) } \over ad -bc})\)

5. If the sum of two numbers is ‘A’ and their difference is ‘x’, then the ratio of numbers is given by (A + x) : (A - x).

 

PROPORTION:

The equality of two ratios is called proportion. If (a : b) = (c : d), we write, (a : b :: c : d) and we say that a, b, c, d are in proportion . Here, ‘a’ and ‘d’ are called extremes, while ‘b’ and ‘c’ are called mean terms.

Note: Product of means = Product of extremes. Thus,

(a : b :: c : d) <=> (b x c) = (a x d);

Generally proportional are two types:

1) Direct Proportional                               2) Indirect Proportional

Direct Proportional: If on the increase/decrease of one quantity, the other quantity also increases/decreases to the same extent, then we say that the given two quantities are directly proportional. If ‘A’ and ‘B’ are directly proportional, then we denote it by \(A ∝B\)

We can represent \((A ∝B)\) as (A = KB), where ‘K’ is proportional constant.

Indirect Proportional (Inverse Proportional): If on the increase of one quantity, the other quantity decreases to the same extent and on the decrease of one, the other increase to the same extent, then we say that the given two quantities are indirectly proportional. If ‘A’ and ‘B’ are indirectly proportional then we denote it by \(A ∝ {1 \over B}\).

We can represent \(A ∝ {1 \over B}\) as \((A = M {1 \over B})\), where’ is proportional constant.

 

Example: - On a crossroad, there are 8 lights which are lightened 8 hours at night. If the power consumed by these lights is 20 watts in 5 days, then how many lights are required on the crossroad to be lightened for a month for only 4 hours in night consuming 30 watts power?

Solution: - let x no. of lights are fitted on the crossroad.

More lights, means more money and more power consumption.

Less hours per day, means less power consumption and less money.

Ratio of power consumed in both cases, is 20 : 30;

Ratio of number of lights is 8 : x; (directly proportional to the power consumption)

Ratio of time for which lights remain ON is  8 : 4; (directly proportional to the power consumption)

Ratio of number of days for which lights are lightened is 5 : 30;  (directly proportional to the power consumption)

The relation between different terms can be established as

\({N_{1}T_{1}D_{1} \over N_{1}T_{1}D_{1}}∝{P_{1} \over P_{1}}\)

Where, N = no of lights,

T = hours,

D = no of days,

P = power consumption.

⇒\({8*8*5 \over x*4*30}={20 \over 30}\)

\(8×8×5×30=x×4×30×20\)

x = 4 light

Thus, only 4 light should be allowed for lighting.

 

Properties of proportional:

1. Fourth Proportional:

If (a : b) = (c : d), then ‘d’ is called the fourth proportional to a, b and c. This relation can also be expressed as \((d={bc \over a})\).

2. Third Proportional:

If (a : b) = (b : c), then c is called the third proportional to a and b. This relation can also be expressed as \( c= {b^2 \over a}\) and ‘b’ is called a mean proportional.

3. (i) Duplicate ratio of (a : b) is a²:b².    

     (ii) Sub-duplicate ratio of (a : b) is \(\sqrt a : \sqrt b\)  

          (iii)Triplicate ratio of (a : b) is a³:b³.   

          (iv) Sub-triplicate ratio of (a : b) is \((a^{1 \over 3}:b^{1 \over 3})\).

 

Rule of three: 

In a problem with direct and indirect proportion, usually, three terms are given and we have to find the fourth term, which we can solve by using Rule of three.

To apply Rule of Three, two of the given terms should be of the same kind and the third term should be of the same kind as the unknown required fourth term.

Note: The same Kind denotes that the quantities should be the same in terms of dimensions and units.

So, let us say a set X : {a, b} comprises of the two terms of the same kind while a set Y : {c, d} comprises of the two terms of the same kind. And, set X is either directly proportional or indirectly proportional to the set Y. In this case, we can apply the Rule of Three.

• In case of direct proportional relationship we use the relation

\({a \over b}={c \over d}\)

• In case of indirect proportional relationship we use the relation

\({a \over b}={d \over c}\)

 

Example: - Rahim works in a construction site. He completes \(3 \over 4\) of a wall in 12 days. Then at this speed, how many days will Rahim take to complete the wall.

Solution: - Rahim completes \(3 \over 4\)of the wall in 12 days, then let remaining part of wall i.e. \(1 \over 4\)of wall will be finished in x more days.

Here in construction of wall and number of days, there is a direct relationship

Thus,

Using the Rule of three

\({3 \over 4}:{1 \over 4}=12:x\)

\({({3 \over 4}) \over ({1 \over 4})}={12 \over x}\)

\(x={({3 \over 4}) \over ({1 \over 4})} * 12 \)

x = 4 days.

 

Ratio and Proportion Examples:

1: - A box is having coins of denomination 50 Paisa, 25 Paisa and 10 paisa. The ratio of the number of coins in the box is 5: 9: 4, respectively. If the total money in the box is Rs.206. Find the number of coins of each type?

Solution: Let the number of 50 Paisa, 25 Paisa and 10 Paisa coins be 5x, 9x and 4x respectively.

50 Paisa = ₹ 0.5, 25 Paisa = ₹ 0.25 & 10 Paisa = ₹ 0.01

Total Amount = (Amount of one coin * Number of coins)

So, (5x) * (0.5) + (9x) * (0.25) + (4x) * (0.01) = 206

⇒ x = 40;

So total 50 p coins are (40 × 5) = 200;

25 p coins are (40 × 9) = 360;

10 p coins are (40 × 4) = 160;

2: - The ratio of water and alcohol in a mixture present in a tank is 3 : 4. If 5 liters of water is added to the tank’s mixture, the ratio becomes 5: 4. Find the quantity of alcohol in the given mixture?

Solution: Let the quantity of alcohol and water be 4x liters and 3x liters, respectively.

5 liters of water is added so net water is (3x + 5);

After adding the 5 liters of water to the old mixture, the ratio changes to (5 : 4)

So,

⇒\({(3x +5) \over (4x)}={5 \over 4}\)

x = 2.5 liter

Thus, quantity of alcohol in the mixer is (2.5 × 4) = 10 liters.

3: - A monkey takes 2 jumps for the 5 jumps made by a deer while a kangaroo takes 7 jumps for the 10 jumps made by a deer in the same time. The distance covered by a monkey in 8 jumps is equal to the distance covered by deer in 2 jumps and distance covered by a kangaroo in 4 jumps. What is the ratio of the distance travelled by monkey, deer and kangaroo?

Solution: -

Ratio of jumps made by monkey and deer will be = 2 jumps : 5 jumps

Ratio of jumps made by deer and kangaroo will be = 10 jumps : 7 jumps …… (1)

Writing the equivalence ratio for jumps made by monkey and deer = 2 (2 jumps : 5 jumps) = 4 jumps : 10 jumps ….. (2)

From (1) and (2)

The ratio of the jumps made by monkey, deer and kangaroo will be = 4 jumps : 10 jumps : 7 jumps

Let us assume total distance covered by monkey, deer and kangaroo in 8 jumps, 2 jumps and 4 jumps respectively be X m.

Now, according to question,

8 jumps of monkey = X m

1 jump of monkey = X/8 m

2 jumps of deer = X m

2 jump of deer = X/2 m

4 jumps of kangaroo = X m

4 jump of kangaroo = X/4 m

Ratio  of distance travelled by monkey, deer and kangaroo in actual terms will be

⇒\(4* {X \over 8}:10* {X \over 2}:7*{X \over 4}\)

⇒\({1 \over 2} :5: {7 \over 4}\)

⇒ 2 : 20 : 7

Share Blog