Basics of Trigonometry, Trigonometric Identities, and Trigonometric Formulas

What is Trigonometry?

Trigonometry is the branch of mathematics that deals with the study of angles and sides of a triangle through different trigonometric ratios. Trigonometry is generally connected with the study of right-angle triangles but also applied to general triangles in the form of sine, cosine, and tangent laws. It is instrumental in astronomical studies and measuring the distance between Astronomical objects. Some significant branches of mathematics like Geometry, calculus, functions, and algebra are dependent on Trigonometry.

So, firstly we will discuss angles and how they are measured:

How Angles are measured?

Angles are measured in both degree and radian.

Most of the calculations in trigonometry are done in radians, so we should know the interconversion of degree and radian.

2π radian = 360⁰

There are majorly six types of trigonometric functions which are used in trigonometry to relate angles and sides in a right-angle triangle. These six functions are sine (represented as sin), cosecant (cosec), cosine (cos), secant (sec), tangent (tan) and cotangent (cot).

The values of these functions are basically calculated using a unit circle. A unit circle is a circle having a radius of 1 unit. Also, co-ordinates of a unit circle are (cos Ɵ, sin Ɵ).

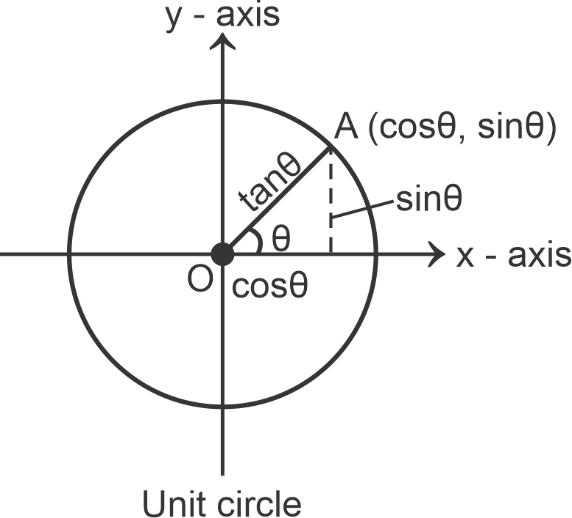
We can calculate the relationship between sides, angles and trigonometric function through a right-angle triangle as follows:

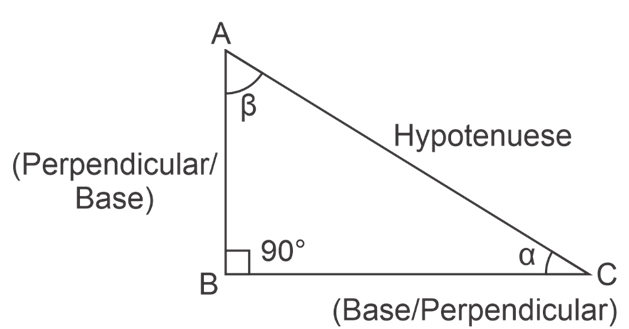
Relationship between Angles, Sides and Trigonometric functions

In a right-angled triangle side opposite to the 90⁰ angle is known as hypotenuse. While side adjacent to the angle in consideration is known as base or adjacent while side opposite to the angle in consideration is known as perpendicular or opposite. Therefore, for angle ‘α’, side BC is the base and side AB is the perpendicular, while for angle ‘β’, side AB is the base and side BC is the perpendicular.

Now, all the trigonometric ratios for ∆ ABC can be defined as:

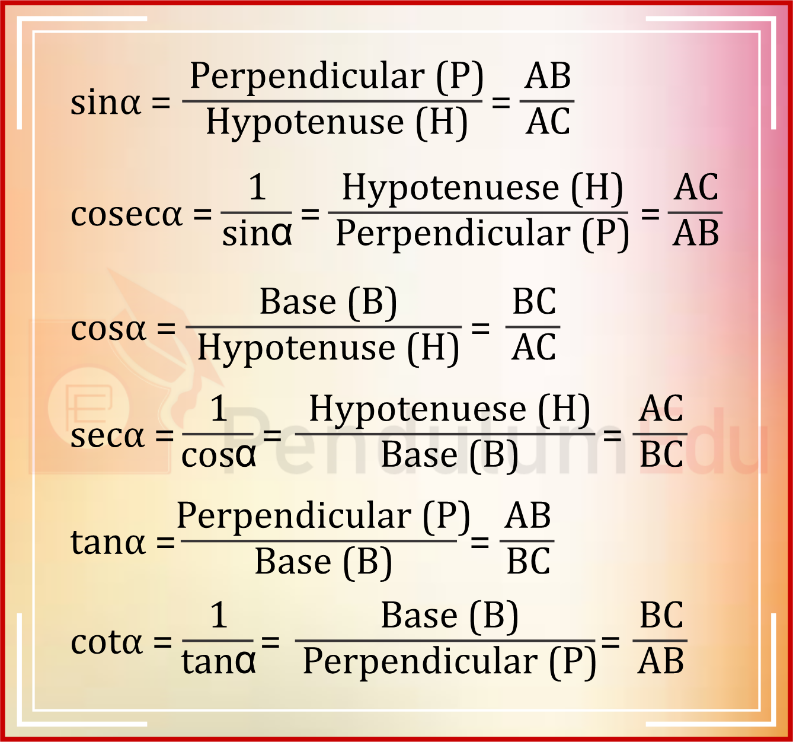
All trigonometric ratios for a right angled triangle

While, when we consider ‘β’ as the angle in consideration, then the trigonometric function will change accordingly.

Important Trigonometric Ratios and Relations

We should remember the values of trigonometric functions for all important angles because without that, we would not be able to solve the questions in the paper. Let us see and learn the values of trigonometric functions at important angles:

Trigonometric Functions	sin	cos	tan	cosec	sec	cot
\(0 ^\circ\) or 0π	0	\(1\)	0	Undefined	\(1\)	undefined
\(30 ^\circ\) or π/6	\(\dfrac{1}{2}\)	\(\dfrac{\sqrt3}{2}\)	\(\dfrac{1}{\sqrt{3}}\)	2	\(\dfrac{2}{\sqrt{3}}\)	\(\sqrt{3}\)
\(45 ^\circ\) or π/4	\(\dfrac{1}{\sqrt{2}}\)	\(\dfrac{1}{\sqrt{2}}\)	\(1\)	\(\sqrt{2}\)	\(\sqrt{2}\)	\(1\)
\(60 ^\circ\) or π/3	\(\dfrac{\sqrt3}{2}\)	\(\dfrac{1}{2}\)	\(\sqrt{3}\)	\(\dfrac{2}{\sqrt{3}}\)	\(2\)	13\(1 \over {\sqrt3}\)
\(90 ^\circ\) or π/2	\(1\)	0	Undefined	1	Undefined	0
\(135 ^\circ\) or 3π/4	\(\dfrac{1}{\sqrt{2}}\)	\(-\dfrac{1}{\sqrt{2}}\)	\(-1\)	\(\sqrt{2}\)	\(-\sqrt{2}\)	\(-1\)
\(180 ^\circ\) or π	0	-1	0	Undefined	-1	undefined
\(225 ^\circ\) or 5π/4	\(-\dfrac{1}{\sqrt{2}}\)	\(-\dfrac{1}{\sqrt{2}}\)	1	\(-\sqrt{2}\)	\(-\sqrt{2}\)	1
\(270 ^\circ\) or 3π/2	\(-1\)	0	Undefined	\(-1\)	Undefined	0
\(315 ^\circ\) or 7π/4	\(-\dfrac{1}{\sqrt{2}}\)	\(\dfrac{1}{\sqrt{2}}\)	-1	\(-\sqrt{2}\)	\(-\sqrt{2}\)	-1
\(360^\circ\) or 2π	0	1	0	Undefined	1	undefined

Other than these values some other values are also asked very frequently in exams;

sin37⁰=\(\dfrac{3}{5}\),cos37⁰=\(\dfrac{4}{5}\) andtan37⁰=\(\dfrac{3}{4}\)

sin53⁰=\(\dfrac{4}{5}\),cos53⁰=\(\dfrac{3}{5}\) andtan53⁰=\(\dfrac{4}{3}\)

sin15⁰=\(\dfrac{{\sqrt3-1}}{{2\sqrt2}}\), cos15⁰=\(\dfrac{{\sqrt3+1}}{{2\sqrt2}}\) andtan15⁰=\(\dfrac{{\sqrt3-1}}{{\sqrt3+1}}\)=\(2-\sqrt3\)

sin75⁰=\(\dfrac{{\sqrt3+1}}{{2\sqrt2}}\), cos75⁰=\(\dfrac{{\sqrt3-1}}{{2\sqrt2}}\) and tan75⁰=\(\dfrac{{\sqrt3+1}}{{\sqrt3-1}}\)=\(2+\sqrt3\)

sin22.5⁰=\(\dfrac{\sqrt{2-\sqrt{2}}}{2}\), cos22.5⁰=\(\dfrac{\sqrt{2+\sqrt{2}}}{2}\) and tan22.5⁰=\(\sqrt2-1\)

Range and Domain of trigonometric functions

Trigonometric function	Range	Domain
sin Ɵ	- 1 to 1	-∞ to ∞
cos Ɵ	- 1 to 1	-∞ to ∞
tan Ɵ	-∞ to ∞	All real no. except π/2 + nπ
cosec Ɵ	(- ∞ to -1) ∪ (1 to ∞)	All real no. except nπ
sec Ɵ	(- ∞ to -1) ∪ (1 to ∞)	All real no. except π/2 + nπ
cot Ɵ	-∞ to ∞	All real no. except nπ

SIGN OF TRIGONOMETRIC FUNCTIONS IN DIFFERENT QUADRANTS

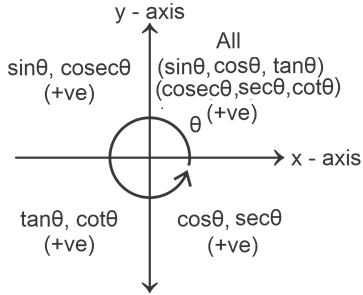
Interconversion of Trigonometric functions

sin (90⁰ – Ɵ) = cos Ɵ

cos (90⁰– Ɵ) = sin Ɵ

sec (90⁰– Ɵ) = cosec Ɵ

cosec (90⁰– Ɵ) = sec Ɵ

tan (90⁰– Ɵ) = cot Ɵ

cot (90⁰– Ɵ) = tan Ɵ

sin (180⁰ – Ɵ) = sin Ɵ

cos (180⁰ – Ɵ) = - cos Ɵ

tan (180⁰ – Ɵ) = - tan Ɵ

NOTE: In case of conversion + and – signs are considered according to the sign of function in a quadrant.

Also, sin (-Ɵ) = - sin Ɵ

cos (-Ɵ) = cos Ɵ

tan (-Ɵ) = - tan Ɵ

cosec (-Ɵ) = - cosec Ɵ

sec (-Ɵ) = sec Ɵ

cot (-Ɵ) = - cot Ɵ

Pythagorean Identities

sin² Ɵ + cos² Ɵ = 1

sec² Ɵ – tan² Ɵ = 1

cosec² Ɵ – cot²Ɵ = 1

Double and triple angle formulae

\(sin 2Ɵ=2 sin Ɵ cos Ɵ=\dfrac{2tanƟ}{1+tan^2Ɵ}\)

\(cos^ 2Ɵ = cos^2 Ɵ – sin^2 Ɵ = 1 – 2 sin2Ɵ = 2cos^² Ɵ – 1\)

\(cos2Ɵ=\dfrac{1-tan^² Ɵ}{1+tan^²Ɵ}\)

\(tan 2Ɵ=\dfrac{2tanƟ}{1-tan^² Ɵ}\)

\(sin 3Ɵ = 3 sin Ɵ – 4 sin^3 Ɵ\)

\(cos 3Ɵ = 4 cos^3 Ɵ – 3 cos Ɵ\)

\(tan3Ɵ=\dfrac{3tanƟ-tan^3Ɵ}{1-3tan^2Ɵ}\)

\(tan\dfrac{Ɵ}{2}=\dfrac{sinƟ}{1+cosƟ}=\dfrac{1-cosƟ}{sinƟ}=\sqrt{\dfrac{1-cosƟ}{1+cosƟ}}\)

SOME USEFUL TRIGONOMETRIC RESULTS AND FORMULAE

Type 1:

sin (A + B) = sin A cos B + cos A sin B

sin (A – B) = sin A cos B – cos A sin B

cos (A + B) = cos A cos B – sin A sin B

cos (A – B) = cos A cos B + sin A sin B

\(tan(A+B)=\dfrac{tanA+tanB}{1-tanAtanB}\)

\(tan(A-B)=\dfrac{tanA-tanB}{1+tanAtanB}\)

\(cot(A+B)=\dfrac{cotAcotB-1}{cotA+cotB}\)

\(cot(A+B)=\dfrac{cotAcotB+1}{cotB-cotA}\)

Type 2:

sin (A + B) + sin (A – B) = 2 sin A cos B

sin (A + B) – sin (A – B) = 2 cos A sin B

cos (A + B) + cos (A – B) = 2 cos A cos B

cos (A + B) – cos (A – B) = – 2 sin A sin B

Type 3:

\(sinA+sinB=2sin(\dfrac{A+B}{2})cos(\dfrac{A-B}{2})\)

\(sinA-sinB=2cos(\dfrac{A+B}{2})sin(\dfrac{A-B}{2})\)

\(cosA+cosB=2cos(\dfrac{A+B}{2})cos(\dfrac{A-B}{2})\)

\(cosA-cosB=2sin(\dfrac{A+B}{2})sin(\dfrac{B-A}{2})\)

Type 4:

sin (A + B) × sin (A – B) = sin² A – sin² B = cos² B – cos² A

cos (A + B) × cos (A – B) = cos² A – sin² B = cos² B – sin² A

Type 5:

sin⁴ Ɵ + cos⁴Ɵ = 1 – 2 sin² Ɵ cos² Ɵ

sin⁶ Ɵ + cos⁶ Ɵ = 1 – 3 sin² Ɵ cos² Ɵ

Type 6:

(sec Ɵ – tan Ɵ) (sec Ɵ + tan Ɵ) = 1

(cosec Ɵ – cot Ɵ) (cosec Ɵ + cot Ɵ) = 1

Type 7:

sin Ɵ sin (60 – Ɵ) sin (60 + Ɵ) =\(1 \over 4\)sin3Ɵ

cos Ɵ cos (60 – Ɵ) cos (60 + Ɵ) =\(1 \over 4\)cos3Ɵ

tan Ɵ tan (60 – Ɵ) tan (60 + Ɵ) = tan 3Ɵ

TYPE 8: If A + B = 45⁰ or π/4

(tan A + 1) (tan B + 1) = 2

(cot A – 1) (cot B – 1) = 2

Type 9: If A + B + C = 180⁰

tan A + tan B + tan C = tan A × tan B × tan C

cot A cot B + cot B cot C + cot C cot A = 1

Type 10:

\(tanA+B+C=\dfrac{tanA+tanB+tanC-tanA\:tanB\:tanC}{1-tanA\:tanB-tanB\:tanC-tanC\:tanA}\)

sin (A + B + C) = sin A cos B cos C + sin B cos A cos C + sin C cos A cos B – sin A sin B sin C

cos (A + B + C) = cos A cos B cos C – cos A sin B sin C – cos B sin A sin C − cos C sin A sin B

MAXIMA AND MINIMA OF SOME GENERAL FUNCTIONS

FUNCTION	MINIMA	MAXIMA
sin² Ɵ, cos² Ɵ	0	1
a.sin Ɵ ± b.cos Ɵ	\(-\sqrt{a^2+b^2}\)	\(\sqrt{a^2+b^2}\)
a.sin Ɵ ± b.sin Ɵ	\(-\sqrt{a^2+b^2}\)	\(\sqrt{a^2+b^2}\)
a.cos Ɵ ± b.cos Ɵ	\(-\sqrt{a^2+b^2}\)	\(\sqrt{a^2+b^2}\)
(sinn Ɵ cosn Ɵ)	If n is even, min = 0 If n is odd, min = -\(({1\over2})^n\)	\(({1\over2})^n\)
a.sin² Ɵ + b.cosec² Ɵ	If a < b Min = a + b If a > b Min=\(2\sqrt{ab}\)	∞
a.cos² Ɵ + b.sec² Ɵ	If a < b Min = a + b If a > b Min=\(2\sqrt{ab}\)	∞
a.tan² Ɵ + b.cot² Ɵ	\(2\sqrt{ab}\)	∞