Limits in Math: What is it, Its Laws, and Calculations

2023-01-31 | Priyanka Chaudhary

In calculus and mathematical analysis, the term limit plays a vital role in defining the continuity, Taylor series, integrals, and differentiation. Limit is a well-known branch of calculus and is used for the calculations of a function at a particular point to check the behavior of the function.

In differentiation, the limit is used in the first principle method to differentiate the functions. While in integration, limits are used in the definite type to integrate the numerical value with the help of the upper and lower limit.

What is the limit?

In mathematics, the limits are the unique real numbers of the functions at a particular point. For the real-valued function “f(x)” at the real point “a”, the limit can be expressed as:

The above expression of the limit can be read as the limit of “f of x”, as “x” approaches “a” equals “M”.

Types of limits

There are three types of limits in mathematics such as:

1. Left-hand limit
2. Right-hand limit
3. Two-sided limit

The limit of the function is said to not exist if the left-hand limit and right-hand limit are not equal. The limit of the function only exists when the left-hand limit is equal to the right-hand limit.

Laws of limits

Here are some laws of limits.

Formulas of limits

Here are some well-known formulas of the limit.

1. Lim_x→b [(xⁿ – bⁿ)/(x – b)] = nb^{(n – 1)}
2. Lim_x→0 [sin(x) / x] = 1
3. Lim_x→0 [tan(x) / x] = 1
4. Lim_x→0 [1 – cos(x) / x] = 0
5. Lim_x→0 [sin(x)] = 0
6. Lim_x→0 [e^x] = 1
7. Lim_x→0 [cos(x)] = 1

How to calculate the limit problems?

Here are a few examples of solving limit problems. The expression and laws of limits play a vital role in the calculations of limit problems.

Example 1

Find the limit value of f(u) = (3u² + 10u – 12) / (4u³ + 2u² – 1) at the specific point “3”.

Solution

Step 1: First of all, write the given function and apply the notation of the limit to it.

Lim_u→a [f(u)] = lim_u→3 [(3u² + 10u – 12) / (4u³ + 2u² – 1)]

Step 2: Apply the laws of limit calculus to the above expression.

According to addition, subtraction, and division laws:

lim_u→3 [(3u² + 10u – 12) / (4u³ + 2u² – 1)] = (lim_u→3 [3u²] + lim_u→3 [10u] – lim_u→3 [12]) / (lim_u→3 [4u³] + lim_u→3 [2u²] – lim_u→3 [1])

According to the constant function law.

lim_u→3 [(3u² + 10u – 12) / (4u³ + 2u² – 1)] = (3lim_u→3 [u²] + 10lim_u→3 [u] – lim_u→3 [12]) / (4lim_u→3 [u³] + 2lim_u→3 [u²] – lim_u→3 [1])

Step 3: Now apply the specific point of limit to the above expression.

lim_u→3 [(3u² + 10u – 12) / (4u³ + 2u² – 1)] = (3 [3²] + 10 [3] – [12]) / (4 [3³] + 2 [3²] – [1])

lim_u→3 [(3u² + 10u – 12) / (4u³ + 2u² – 1)] = (3 [3 x 3] + 10 [3] – [12]) / (4 [3 x 3 x 3] + 2 [3 x 3] – [1])

lim_u→3 [(3u² + 10u – 12) / (4u³ + 2u² – 1)] = (3 [9] + 10 [3] – [12]) / (4 [27] + 2 [9] – [1])

lim_u→3 [(3u² + 10u – 12) / (4u³ + 2u² – 1)] = (27 + 30 – 12) / (108 + 18 – 1)

lim_u→3 [(3u² + 10u – 12) / (4u³ + 2u² – 1)] = (57 – 12) / (126 – 1)

lim_u→3 [(3u² + 10u – 12) / (4u³ + 2u² – 1)] = (45) / (125) = 9/25

lim_u→3 [(3u² + 10u – 12) / (4u³ + 2u² – 1)] = 0.36

Online tools can also be used to evaluate the result of limit problems with steps in no time. Let us solve the above problem using an online tool.

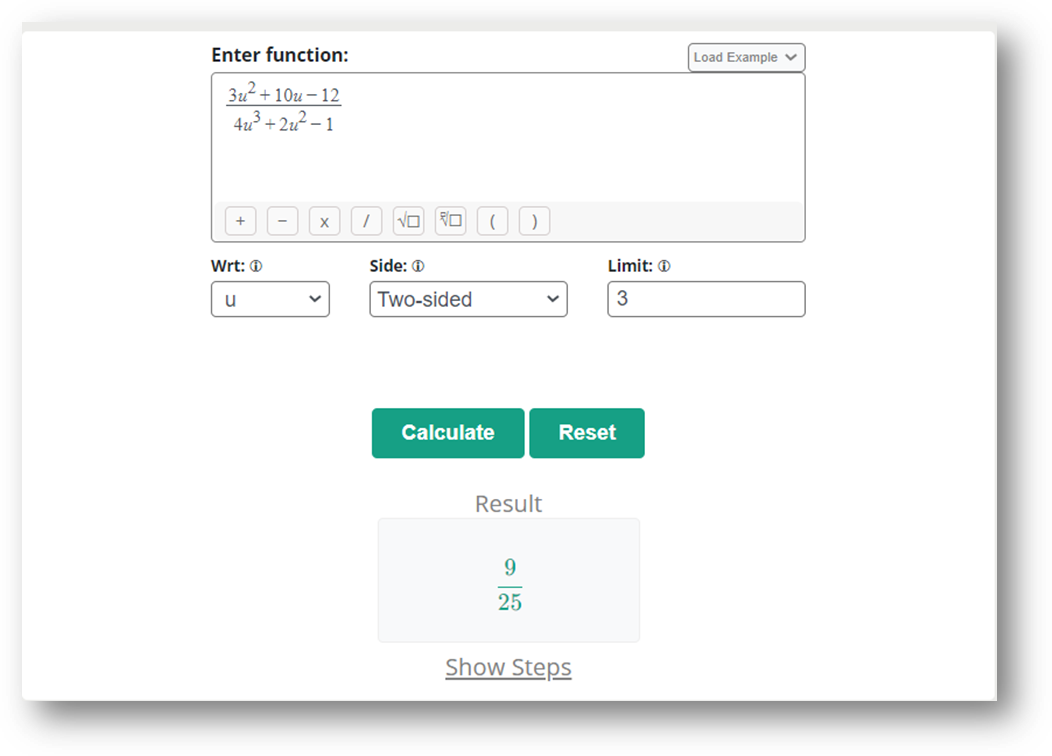
Problem solve by [https://www.allmath.com/limit-calculator.php]

Example 2:

Find the limit value of f(v) = v⁴ + 2v² – 3 / (6v³ – 6) if the particular value is 1.

Solution

Step 1: First of all, write the given function and apply the notation of the limit to it.

f(v) = v⁴ + 2v² – 3 / (6v³ – 6)

lim_v→a [f(v)] = lim_v→1 [v⁴ + 2v² – 3 / (6v³ – 6)]

Step 2: Apply the laws of limit calculus to the above expression.

According to addition, subtraction, and division laws:

lim_v→1 [v⁴ + 2v² – 3 / (6v³ – 6)] = (lim_v→1 [v⁴] + lim_v→1 [2v²] – lim_v→1 [3]) / (lim_v→1 [6v³] – lim_v→1 [6])

According to the constant function law.

lim_v→1 [v⁴ + 2v² – 3 / (6v³ – 6)] = (lim_v→1 [v⁴] + 2lim_v→1 [v²] – lim_v→1 [3]) / (6lim_v→1 [v³] – lim_v→1 [6])

Step 3: Now apply the specific point of limit to the above expression.

lim_v→1 [v⁴ + 2v² – 3 / (6v³ – 6)] = ([1⁴] + 2 [1²] – [3]) / (6 [1³] – [6])

lim_v→1 [v⁴ + 2v² – 3 / (6v³ – 6)] = (1 + 2 [1] – [3]) / (6 [1] – [6])

lim_v→1 [v⁴ + 2v² – 3 / (6v³ – 6)] = (1 + 2 – 3) / (6 – 6)

lim_v→1 [v⁴ + 2v² – 3 / (6v³ – 6)] = 0/0

Step 3: Apply L’hopital’s rule of limit as the function gives 0/0 form. Now find the derivative of the function and apply the limit value again.

lim_v→1 [v⁴ + 2v² – 3 / (6v³ – 6)] = lim_v→1 [d/dv (v⁴ + 2v² – 3) / d/dv (6v³ – 6)]

lim_v→1 [v⁴ + 2v² – 3 / (6v³ – 6)] = lim_v→1 [(4v³ + 4v – 0) / (18v² – 0)]

lim_v→1 [v⁴ + 2v² – 3 / (6v³ – 6)] = lim_v→1 [(4v³ + 4v) / (18v²)]

apply v = 1

lim_v→1 [v⁴ + 2v² – 3 / (6v³ – 6)] = (lim_v→1 [4v³] + lim_v→1 [4v]) / (lim_v→1 [18v²])

lim_v→1 [v⁴ + 2v² – 3 / (6v³ – 6)] = ([4(1)³] + [4(1)]) / ([18(1)²])

lim_v→1 [v⁴ + 2v² – 3 / (6v³ – 6)] = ([4(1)] + [4(1)]) / ([18(1)])

lim_v→1 [v⁴ + 2v² – 3 / (6v³ – 6)] = (4 + 4) / (18)

lim_v→1 [v⁴ + 2v² – 3 / (6v³ – 6)] = 8/18

lim_v→1 [v⁴ + 2v² – 3 / (6v³ – 6)] = 0.45

Sum Up

Now you can take all the assistance of limit in mathematics from this article. The limit is a well-known branch of calculus that deals with the value of the functions at a particular point.

0 LIKES

0

COMMENTS

Comments

COMMENT

Share Blog