QOTD-Geometry-Find the length of side SB

2019-07-03 | Team PendulumEdu

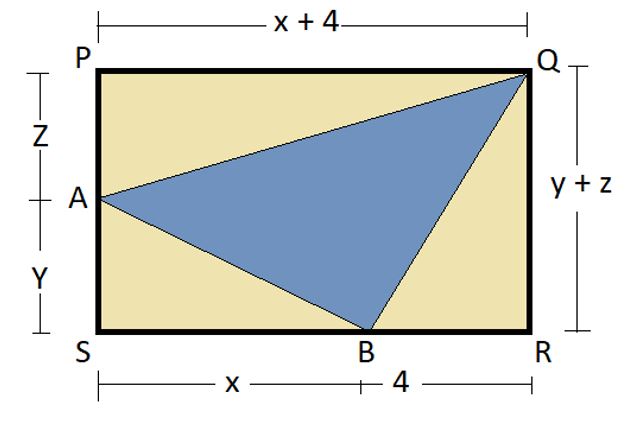
A rectangular plane is cut into four triangles in such a way that the area of triangle APQ, ASB and BRQ is equal. Length of side BR is 4 cm. Find the length of SB.

A. \((1+2\sqrt{5})m\)

B. \((\sqrt{5}-2)m\)

C. \(2(\sqrt{5}-1)m\)

D. \(2(1+\sqrt{5})m\)

Solution

Let the length of side SB = x

Length of side AS = y

Length of side PA = z

So, now \(PQ = x + 4\) and\( QR = y + z\)

According to the question

Area of triangle APQ = Area of triangle ASB = Area of triangle BRQ

\(\frac{1}{2}* z* (x+4)= \frac{1}{2} * y* x = \frac{1}{2}* (y+z)* 4\)

\(z*(x+4)= y+z* 4\)……………………………..(1)

\(z*x+4= y*x\) ……………………………………….(2)

Using equation (1), we get

\(4y+4z=zx+4z\)

\(Z=\frac{4y}{x}\)

Now, substituting the value of z in equation (2), we get

\(\frac{4y}{x}*(x+4)=x*y\)

\(x^{2} - 4x - 16=0\)

\(x=2(1\pm\sqrt{5})\)

Length cannot be negative, therefore \( SB=2(1+\sqrt{5})\)

Hence, (d) is the correct option.

This type of question is asked in the Quantitative Aptitude section of different competitive exams like SSC CGL, SSC CHSL, IBPS PO, RRB JE, RRB NTPC, RRC Group D, CAT, etc. Therefore, one can try and practice our free mock tests at PendulumEdu and find out the easiest and quick way to solve such questions.

Previous Next

0 LIKES