Find the area of the triangle formed by the straight line x – y = 2 , x + 2y = 8 and y- axis.
Answer
Correct Answer : a ) 12 sq. unit
Explanation :According to the question
Straight lines are:
x – y = 2……..(1)
x + 2y = 8…….(2)
x = 0……….(3)
Now to find the area of the triangle, we need to find the coordinates of the vertices of the triangle.
Point at which line 1 and 2 intersect:
Subtracting eq(1) form eq (2)
⇒ 3y = 6
⇒ y = 2
⇒ x – y = 2
⇒ x = 2 + 2
⇒ x = 4
⇒ Both the lines intersect at (4, 2)
Point at which line 1 and 3 intersect:
x = 0 and y = -2
Point at which line 2 and 3 intersect:
x = 0 and y = 4
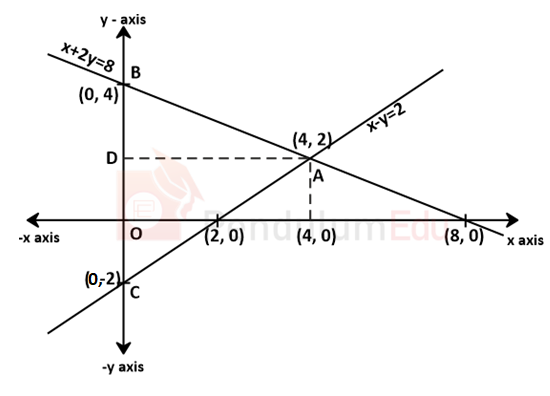
As shown in figure
Area of △ABC
Height AD = 4 units
Base (BC) = 4 + 2
⇒ 6 units
Area of triangle=\({1 \over 2}\)*base*height
⇒\({1 \over 2}*6*4\)
⇒ 12 sq. units
Hence, (a) is the correct answer.
Share QOTD
Popular Blog
Highlights of Interim Budget 2024
Read More
150+ Paryayvachi Shabd in Hindi - पर्यायवाची शब्द
Read More
Highlights of G20 Summit 2023
Read More
SSC CHSL Tier 1 Exam Analysis 2023 - Questions Asked from 2 to 22 August 2023
Read MoreLatest Current Affairs
Daily Current Affairs and GK | 26 and 27 April 2024
Read More
Daily Current Affairs and GK | 25 April 2024
Read More
Daily Current Affairs and GK | 24 April 2024
Read More
Daily Current Affairs and GK | 23 April 2024
Read More
Daily Current Affairs and GK | 21 and 22 April 2024
Read More
Comments