In the given figure, AB and MN are two chords such that, AB = 58 cm and CD = 42 cm. What is the value of MN?
Answer
Correct Answer : c ) 40 cm
Explanation :According to the question
Let, ‘O’ be the center of the concentric circles, ‘r’ and ‘R’ be the radius of smaller and larger circle
Respectively,
OE is drawn perpendicular to AB and let OE be ‘h’
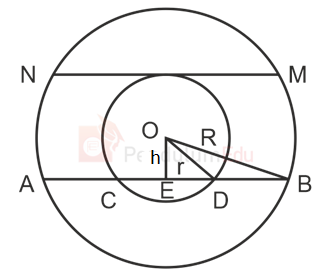
We know that,
If a perpendicular is drawn from the center to any chord of the circle, then it bisects the chord and vice versa.
⇒ED=\(CD \over 2\)=\(42 \over 2\)
⇒ ED = 21 cm
Similarly,
⇒EB=\(AB \over 2\)=\(58 \over 2\)
⇒ EB = 29 cm
In ∆OED (using Pythagoras theorem)
⇒ OD2 = OE2 + ED2
Substituting the values
⇒ r2 = h2 + 212………..(1)
In ∆OEB (using Pythagoras theorem)
⇒ OB2 = OE2 + EB2
⇒ R2 = h2 + 292……….(2)
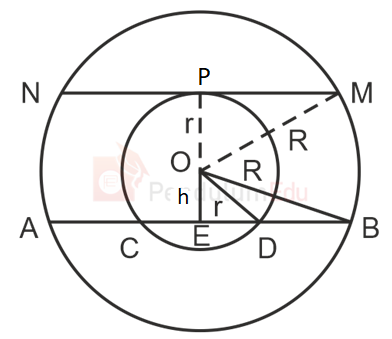
In △OPM (using Pythagoras theorem)
OM2 = OP2 + PM2
Substituting the values
⇒ R2 = r2 + PM2
⇒ PM2 = R2 – r2
Substituting the values for eq(1) and eq (2)
⇒ PM2 = (h2 + 292) – (h2 + 212)
⇒ PM2 = h2 + 292 – h2 – 212
⇒ PM2 = 292 – 212
⇒ PM2 = 400
⇒PM=\(\sqrt {400}\)
⇒ PM = 20 cm
⇒ NM = 2PM
⇒ NM = 2 * 20
⇒ NM = 40 cm
Hence, (c) is the correct answer.
Share QOTD
Popular Blog
Highlights of Interim Budget 2024
Read More
150+ Paryayvachi Shabd in Hindi - पर्यायवाची शब्द
Read More
Highlights of G20 Summit 2023
Read More
SSC CHSL Tier 1 Exam Analysis 2023 - Questions Asked from 2 to 22 August 2023
Read More
Comments