QOTD | Quantitative Aptitude | Mensuration

Question of The Day02-03-2020

In an arrangement of two concentric circles, a chord (length = 10 cm) for the bigger circle is the tangent for the smaller circle. If the diameter of the smaller circle is 6 cm, then what will be the ratio of the areas of the bigger circle to that of the smaller circle?

Answer

Correct Answer : d ) 34:9

Explanation :

Let the radius of the bigger and smaller circles be R and r

Depicting the information given in the question into a figure we get

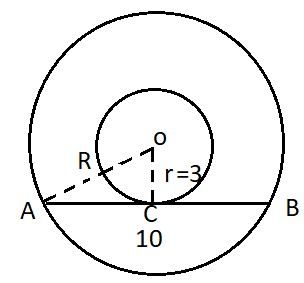
As, tangent makes an angle of \(90^{\circ}\) with the radius of the circle touching the point of tangency

So, OC will be the perpendicular on AB

As, we know in any circle the perpendicular drawn from the center to any chord will divide the chord into 2 equal parts.

Thus, AC = CB = 5 cm

Now, using Pythagoras theorem in triangle OAC

\(OA^{2} = OC^{2} + CA^{2}\)

\(R^{2} = r^{2} + 5^{2}\)

\(r^{2}(\frac{R^{2}}{r{2}}-1)=25\)

\(\frac{R^{2}}{r{2}}=\frac{25}{9}+1\)

\(\frac{R^{2}}{r{2}}=\frac{34}{9}\)

\(\frac{\Pi R^{2}}{\Pi r{2}}=\frac{34}{9} \)

Thus, the ratio of the area of bigger to the smaller circle will be 34: 9.

Hence, (d) is the correct answer.

Such type of question is asked in various government exams like SSC CGL, SSC MTS, SSC CPO, SSC CHSL, RRB JE, RRB NTPC, RRB GROUP D, RRB OFFICER SCALE-I, IBPS PO, IBPS SO, RRB Office Assistant, IBPS Clerk, RBI Assistant, IBPS RRB OFFICER SCALE 2&3, etc.

Read Daily Current Affairs, Banking Awareness, Hindi Current Affairs, Word of the Day, and attempt free mock tests at PendulumEdu and boost your preparation for the actual exam.