Answer

Correct Answer : a ) 8

Basic Method:

Time Taken by A to complete the work = 35 days

Work done by A in 1 day = \(1 \over 35\) units

Time Taken by B to complete the work = 40 days

Work done by B in 1 day = \(1\over40\) units

Work done by A and B together in 1 day (Efficiency of A and B together):

⇒\(1 \over 35\)+ \(1\over40\)= \(15\over280\)

B work alone for 23 days

Work done by B in 23 days= \(23 \over 40\) units

Assume the complete work being done is 1

Work done by A and B together= 1- \(23 \over 40\)=\(17 \over 40\)

Time taken to complete the work= \(Total work \over Efficiency\)

Time taken by A and B to do 17/40 units of work = \({{17\over40}\over{15\over280}}={{17*280}\over{40*15}}\)

⇒ 7.9333 days (Approx. ≈8 days)

Therefore, A left the work after 8 days.

Alternative Method:

Time Taken by A to complete the work = 35 days

Time Taken by B to complete the work = 40 days

Let’s assume total work done by A and B = LCM (35, 40) = 280

Work done by A in 1 day= \(280 \over 35\)=8 units 

Time Taken by B to complete the work = 40 days

Work done by B in 1 day= \(280\over 40\)=7 units 

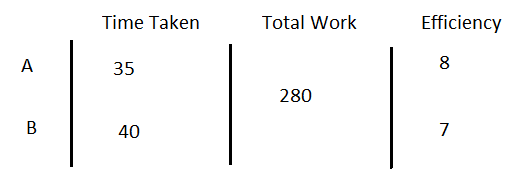
B work alone for 23 days

Work done by B alone = 23*7 = 161

Remaining work done by A and B together = 280-161 = 119

Work done by A and B together in 1 day = 8 + 7 = 15 units

Time taken by A and B to do the remaining work:

 ⇒\(119 \over 15\)=7.93333..     (Approx. ≈8) 

Therefore, A left the work after 8 days.

Hence, (a) is the correct answer.