Relative Speed Practice Question of Train and Man standing on a Platform

Question of The Day13-06-2022

If two men A and B are walking on the platform in the west direction with the speed of 4 km/h and 6 km/h. A train approaching them from behind crosses A in 18 sec and B in 20 sec. Then find the speed and length of train.

Answer

Correct Answer : b ) 24 km/h , 100 m

Explanation :

Let us visualize the information given in the question through the following diagram:

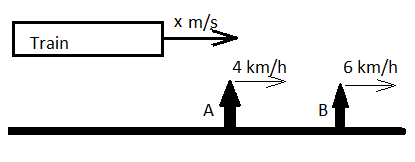
As time is given in seconds. So to keep our calculations easy we are converting speed of A and B from km/h to m/s

Speed of A is 4 km/h

Speed of A in m/s= 4 * \(5\over18\) = \(10\over9\)m/s

Speed of B is 6 km/h

Converting above speed in m/s = \(6*{5\over18}\)=\(5\over3\) m/s

Let the speed of the train be x m/s.

Relative speed of train w.r.t. A = \({(x- {10\over9})}\) m/s

Relative speed of train w.r.t. B = \((x- {5\over3})\) m/s

Distance travelled by the train to cross both men will be equal to the length of train (In such cases, the length of the object being crossed is considered negligible).

Length of Train = Relative speed of train w.r.t. A * Time taken to cross A = Relative speed of train w.r.t. B * Time taken to cross B

\({(x- {10\over9})*18}={(x-{5\over3})*20}\)

27x – 30 = 30x – 50

x=\(20 \over 3\)m/s

Since options are given in km/h. Let’s convert the speed of the train in km/h.

Speed of train in km/h = \({20 \over 3}*{18\over5}\) km/h=24 km/h

Length of train = Relative speed of train w.r.t. A * Time taken to cross A

Therefore, length of train = \({({20\over3}- {10\over9})*18}\)=100 m

Hence, B is the correct answer.