QOTD | Quantitative Aptitude | Mensuration

Question of The Day19-03-2020

A conical tent has a circumference of 88 m and a height of 2 m. What will be the cost of making the tent if the cost of the cloth is Rs. 5/m²?

Answer

Correct Answer : b ) ₹ \(2200\sqrt{2}\)

Explanation :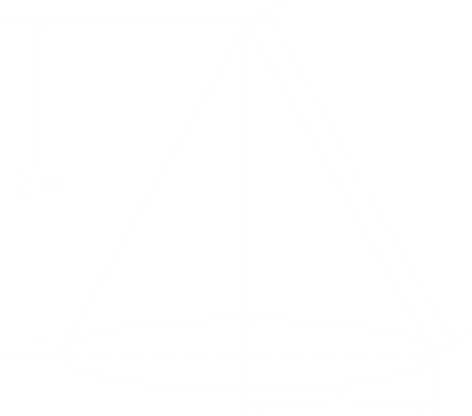

QOTD Solution 19 March

We know that the base of the cone is a circle.

So, the circumference of the cone = 2πr

According to the question,

2πr = 88 m

r = 14 m

Now, Applying Pythagoras theorem in the triangle ADC

\(l= {\sqrt{(h^2+r^2)}}\)

\(l=10\sqrt{2} \) m

As the Base will remain open in case of tent, thus the total surface area of the tent will be equal to the curved surface area of the tent.

Thus, total curved surface area of the cone = πrl

⇒\({ 22\over 7}*14*10 \sqrt{2}=440 \sqrt{2} \) m²

Therefore, the cost of making the cloth will be = \(5* 440 \sqrt{2} =\)₹ \(2200{\sqrt{2}}\)

Hence, (b) is the correct answer.

Such type of question is asked in various government exams like SSC CGL, SSC MTS, SSC CPO, SSC CHSL, RRB JE, RRB NTPC, RRB GROUP D, RRB OFFICER SCALE-I, IBPS PO, IBPS SO, RRB Office Assistant, IBPS Clerk, RBI Assistant, IBPS RRB OFFICER SCALE 2&3, UPSC CDS etc.

Read Daily Current Affairs, Banking Awareness, Hindi Current Affairs, Word of the Day, and attempt free mock tests at PendulumEdu and boost your preparation for the actual exam.