Answer

Correct Answer : b ) \(\frac{2}{\sqrt{5}}\: r \)

Depicting the given information in the figure, we get

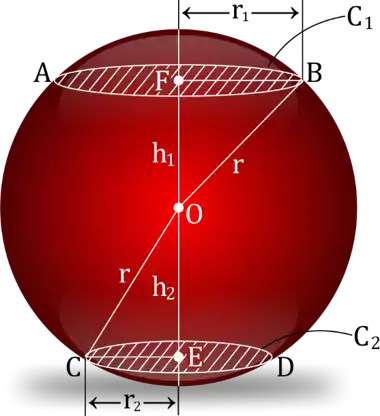
According to the question, the total surface area of the resulting figures is increased by 2πr². As increase in the area can only be because of addition of the new circular faces created because of the two cuts, therefore,

Increase in Total surface area of Sphere = 2* (Area of C₁ + Area of C₂)

2πr² = 2πr₁² + 2πr₂²

r₁² + r₂² = r²........... (1)

Now, applying Pythagoras theorem in Δ OFB

r₁² = r² – h₁².......... (2)

And, applying Pythagoras theorem in Δ OEC

r₂² = r² – h₂².......... (3)

Putting the values of r₁ and r₂ from equation 2 and 3 in equation 1, we get

r² – h₁² + r² – h₂² = r²

h₂² + h₁² = r²..... (4)

As, ratio of the heights h₁ and h₂ is 1 : 2 So,

\(\frac{h_{1}}{h_{2}}\: = \frac{1}{2}\: \) ........(5)

From equation 4 and 5, we get

\(h_{2}\, ^{2}+\: \frac{1}{4}{h_{2}\, ^{2}}\: = r^{2}\)

\(h_{2}\, =\frac{2}{\sqrt{5}}\: r \)

Hence, (b) is the correct answer.

Questions related to Mensuration are asked in competitive exams like SSC CGL, SSC MTS, SSC CPO,  SSC CHSL, RRB JE, RRB NTPC, RRB GROUP D, RRB OFFICER SCALE-I, IBPS PO, IBPS SO, RRB Office Assistant, IBPS Clerk, RBI Assistant, IBPS RRB OFFICER SCALE 2&3, etc.

Read Daily Current Affairs, Banking Awareness, Hindi Current Affairs, Word of the Day, and attempt free mock tests at PendulumEdu and boost your preparation for the actual exam.